Prove that $\int_0^{+\infty} \frac{\ln x}{a^2+x^2} dx = \frac{\pi\ln a}{2a}$

Question

Is that true $$\int_0^{+\infty} \cfrac{\ln x}{a^2+x^2} dx = \cfrac{\pi\ln a}{2a},$$ where $a>0$ ? And how to compute it?

Answer 1

Putting $x=a\tan t,dx=a\sec^2tdt$ and $x=0\implies t=0, x=\infty\implies t=\frac\pi2$

$$\int_0^{+\infty} \cfrac{\ln x}{a^2+x^2} \, dx=\frac1a\int_0^{\frac\pi2}\ln(a\tan t)\,dt$$

$$\int_0^{\frac\pi2}\ln(a\tan t)dt=\ln a\int_0^{\frac\pi2}\, dt+\int_0^{\frac\pi2}\ln \tan t \, dt$$

Now,

$$\int_0^{\frac\pi2}\ln \tan t \,dt$$ $$=\int_0^{\frac\pi2}\ln \tan (\frac\pi2+0-t) \,dt$$

(as $\int_a^bf(a+b-x)dx=\int_b^af(t)(-dt)$ (putting $a+b-x=t$)

$\int_a^bf(a+b-x)dx=\int_a^bf(t)dt=\int_a^bf(x)dx$)

$$=\int_0^{\frac\pi2}\ln \cot t dt$$ $$=-\int_0^{\frac\pi2}\ln \tan t\,dt\implies \int_0^{\frac\pi2}\ln \tan t\, dt=0$$

and

$$\int_0^{\frac\pi2} \,dt=t\mid _0^{\frac\pi2}=\frac\pi2$$

Answer 2

This integral can be easiest integrated using the method explained here.

Define the function $$f(z) = \frac{\ln^2 z}{a^2+z^2}.$$ With the branch cut of the logarithm along the negative real axis, we choose the keyhole contour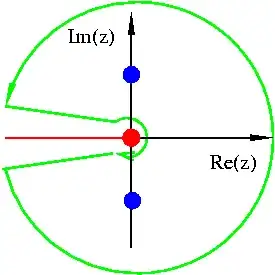

It is easy to check that the function falls of at $\infty$ sufficiently fast that there is no contribution from the large circle. The integration along the branch cut yields $$4\pi i \int_0^\infty \frac{\ln x}{a^2+x^2} dx$$ which has to be the same as the contribution from the residue at $x=\pm ia$, $$2\pi i [ \mathop{\rm Res}_{x=a} f(z) + \mathop{\rm Res}_{x=-a} f(z) ] = \frac\pi{a} \underbrace{[\ln^2(ia) - \ln^2(-ia)]}_{=2i\pi\ln a}.$$

So we have $$\int_0^\infty \frac{\ln x}{a^2+x^2} dx = \frac{\pi \ln a}{2 a}.$$

Answer 3

Take the following complex contour:

$$C_R:=[-R,R]\cup\gamma_R:=\{z\in\Bbb C\;;\;z=Re^{it}\,\,,\,0\leq t\leq \pi\}$$

Within the above path the function has one simple pole, $\,z= ai\,$ (note that $\,z=0\, $ is not a pole. Why?), and

$$Res_{z=ai}(f)=\lim_{z\to ai}\frac{(z-i\sqrt a)Log(z)}{a^2+z^2}=\frac{Log(ai)}{2ai}=\frac{\log a+\frac{\pi i}{2}}{2ai}$$

when we denote $\,Log (z)=$ the complex logarithm, and $\,\log z=$ the real one.

We also have, by Cauchy's estimation formula, that

$$\left|\int_{\gamma_R}\frac{Log(z)}{z^2+a^2}dz\right|\leq \max_{z\in\gamma_R}\frac{|Log(z)|}{|z^2+a^2|}\cdot\pi R\leq \frac{\sqrt 2\,\pi R\log R}{R^2-a^2}\xrightarrow [R\to\infty]{} 0$$

since $|Log (z)|=|\log z+i\arg z|=\sqrt{\log^2R+\arg^2(z)}\leq\sqrt{\log^2R+\pi^2}\leq\sqrt 2\,\log R\,$

for $\,R\,$ big enough.

Thus, using Cauchy's Residue theorem and then passing to the limit:

$$2\pi i\frac{\log a+\frac{\pi i}{2}}{2ai}=\oint_{C_R}f(z)\,dz=\int_{-R}^R\frac{\log |x|}{x^2+a^2}dx+\int_{\gamma_R}f(z)\,dz\xrightarrow[R\to\infty]{} \int_{-\infty}^\infty\frac{\log |x|}{x^2+a^2}dx$$

Since the last integral's integrand function is even, and comparing real and imaginary parts, we get:

$$\int_0^\infty\frac{\log x}{x^2+a^2}dx=\frac{\pi\,\log a}{2a}$$

Answer 4

Consider the parameter-dependent integral:

$$I(a,b)=\int_0^{\infty}\frac{\ln(b^2+x^2)}{a^2+x^2}dx$$

Let's differentiate with respect to $b$:

$$\frac{\partial I(a,b) }{\partial b}=\int_0^{\infty}\frac{2b}{(b^2+x^2)(a^2+x^2)}dx=\frac{\pi}{a(a+b)}$$

Now, let's integrate the last with respect to $b$:

$$I(a,b)=\pi\frac{\ln(a+b)}{a}+C$$

$C=0$ because $I(\infty,b)=0$

And the original integral:

$$I=\frac{1}{2}I(a,0)=\frac{\pi}{2}\frac{\ln a}{a}$$

Answer 5

Let $$ \mathcal{I}(a)=\int_0^\infty\frac{\ln x}{x^2+a^2}\ dx. $$ Using substitution $u=\dfrac{a^2}{x}\;\Rightarrow\;x=\dfrac{a^2}{u}\;\Rightarrow\;dx=-\dfrac{a^2}{u^2}\ du$ yields \begin{align} \mathcal{I}(a)&=\int_0^\infty\frac{\ln \left(\dfrac{a^2}{u}\right)}{\left(\dfrac{a^2}{u}\right)^2+a^2}\cdot \dfrac{a^2}{u^2}\ du\\ &=\int_0^\infty\frac{2\ln a-\ln u}{a^2+u^2}\ du\\ &=2\ln a\int_0^\infty\frac{1}{a^2+u^2}\ du-\int_0^\infty\frac{\ln u}{u^2+a^2}\ du\\ \color{red}{\mathcal{I}(a)}&=2\ln a\int_0^\infty\frac{1}{a^2+u^2}\ du-\color{red}{\mathcal{I}(a)}\\ \mathcal{I}(a)&=\ln a\int_0^\infty\frac{1}{a^2+u^2}\ du. \end{align} The last integral can easily be evaluated since it is a common integral. Using substitution $u=\tan\theta$, the integral turns out to be \begin{align} \mathcal{I}(a)&=\frac{\ln a}{a}\int_0^{\Large\frac\pi2} \ d\theta\\ &=\large\color{blue}{\frac{\pi\ln a}{2a}}. \end{align}

Answer 6

Another approach :

Consider $$ \int_0^\infty\frac{x^{b-1}}{a^2+x^2}\ dx.\tag1 $$ Rewrite $(1)$ as \begin{align} \int_0^\infty\frac{x^{b-1}}{a^2+x^2}\ dx&=\frac1{a^2}\int_0^\infty\frac{x^{b-1}}{1+\left(\frac{x}{a}\right)^2}\ dx.\tag2 \end{align} Putting $x=ay\;\color{blue}{\Rightarrow}\;dx=a\ dy$ yields \begin{align} \int_0^\infty\frac{x^{b-1}}{a^2+x^2}\ dx&=a^{b-2}\int_0^\infty\frac{y^{b-1}}{1+y^2}\ dy, \end{align} where \begin{align} \int_0^\infty\frac{y^{b-1}}{1+y^2}\ dy=\frac{\pi}{2\sin\left(\frac{b\pi}{2}\right)}. \end{align} Hence \begin{align} \int_0^\infty\frac{x^{b-1}}{a^2+x^2}\ dx&=\frac\pi2\cdot\frac{a^{b-2}}{\sin\left(\frac{b\pi}{2}\right)}.\tag3 \end{align} Differentiating $(3)$ with respect to $b$ and setting $b=1$ yields \begin{align} \int_0^\infty\frac{\partial}{\partial b}\left[\frac{x^{b-1}}{a^2+x^2}\right]_{b=1}\ dx&=\frac\pi2\frac{\partial}{\partial b}\left[\frac{a^{b-2}}{\sin\left(\frac{b\pi}{2}\right)}\right]_{b=1}\\ \int_0^\infty\frac{\ln x}{x^2+a^2}\ dx&=\large\color{blue}{\frac{\pi\ln a}{2a}}. \end{align}

Answer 7

$\newcommand{\+}{^{\dagger}} \newcommand{\angles}[1]{\left\langle\, #1 \,\right\rangle} \newcommand{\braces}[1]{\left\lbrace\, #1 \,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\, #1 \,\right\rbrack} \newcommand{\ceil}[1]{\,\left\lceil\, #1 \,\right\rceil\,} \newcommand{\dd}{{\rm d}} \newcommand{\down}{\downarrow} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,{\rm e}^{#1}\,} \newcommand{\fermi}{\,{\rm f}} \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,} \newcommand{\half}{{1 \over 2}} \newcommand{\ic}{{\rm i}} \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow} \newcommand{\isdiv}{\,\left.\right\vert\,} \newcommand{\ket}[1]{\left\vert #1\right\rangle} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\pars}[1]{\left(\, #1 \,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}} \newcommand{\root}[2][]{\,\sqrt[#1]{\vphantom{\large A}\,#2\,}\,} \newcommand{\sech}{\,{\rm sech}} \newcommand{\sgn}{\,{\rm sgn}} \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert} \newcommand{\wt}[1]{\widetilde{#1}}$ $\ds{\int_{0}^{\infty}{\ln\pars{x} \over a^{2} + x^{2}}\,\dd x ={\pi\ln\pars{\verts{a}} \over 2\verts{a}}\,,\qquad a \in {\mathbb R}}$.

With $\ds{R >0}$:

\begin{align} &\color{#c00000}{\int_{0}^{R}{\ln\pars{x} \over a^{2} + x^{2}}\,\dd x} ={1 \over \verts{a}}\,\Im\int_{0}^{R}{\ln\pars{x} \over -\verts{a}\ic + x}\,\dd x =-\,{1 \over \verts{a}}\,\Im\int_{0}^{-\ic R/\verts{a}} {\ln\pars{\verts{a}\ic x} \over 1 - x}\,\dd x \\[3mm]&={1 \over \verts{a}}\Im\braces{\ln\pars{1 + {R \over \verts{a}}\,\ic}\ln\pars{\verts{a}\ic\bracks{-\,{R \over \verts{a}}\,\ic}} -\int_{0}^{-\ic R/\verts{a}}\ln\pars{1 - x}\,{1 \over x}\,\dd x} \\[3mm]&={1 \over \verts{a}}\arctan\pars{R \over \verts{a}}\ln\pars{R} + {1 \over \verts{a}}\Im\int_{0}^{-\ic R/\verts{a}}{{\rm Li}_{1}\pars{x} \over x} \,\dd x \\[3mm]&={1 \over \verts{a}}\arctan\pars{R \over \verts{a}}\ln\pars{R} + {1 \over \verts{a}}\Im\int_{0}^{-\ic R/\verts{a}} \totald{{\rm Li}_{2}\pars{x}}{x}\,\dd x \end{align} where we used well known properties of the PolyLogarithm Functions $\ds{{\rm Li}_{\rm s}\pars{z}}$.

$$\color{#c00000}{\int_{0}^{R}{\ln\pars{x} \over a^{2} + x^{2}}\,\dd x} ={1 \over \verts{a}}\arctan\pars{R \over \verts{a}}\ln\pars{R} + {1 \over \verts{a}}\Im{\rm Li}_{2}\pars{-\,{R \over \verts{a}}\,\ic} $$

With the Inversion Formula ( see the above link ): \begin{align} &\color{#c00000}{\int_{0}^{\infty}{\ln\pars{x} \over a^{2} + x^{2}}\,\dd x} ={1 \over \verts{a}}\lim_{R \to \infty}\braces{\arctan\pars{R \over \verts{a}}\ln\pars{R} - \half\,\Im\bracks{\ln^{2}\pars{{R \over \verts{a}}\,\ic}}} \\[3mm]&={1 \over \verts{a}}\lim_{R \to \infty}\braces{% {\pi \over 2}\,\ln\pars{R} - \half\bracks{\pi\ln\pars{R \over \verts{a}}}} \end{align}

$$ \color{#66f}{\large\int_{0}^{\infty}{\ln\pars{x} \over a^{2} + x^{2}}\,\dd x ={\pi \over 2}\,{\ln\pars{\verts{a}} \over \verts{a}}} $$