6

I am a first-year undergraduate student. I came up with a kind of center property which I cannot find in articles online. I found the center on my own but needed help of mathematicians (@Rahul) on this site.

Currently I'm unsure whether it applies for non-star or open curves. For now, I'm limiting the scope of the definition.

Edit: The function $\overline{r}(x,y)$ may have more than one maximum. Another possibility is to take the average of the maximums. Hence the following is not a center but a property.

However, I would like to know of other possible centers.

Suppose the curve is star-shaped with respect to this center point(s) $\mathbf{p}$ so that any ray emanating from $\mathbf p$ meets the curve exactly once, at say point $\mathbf q$. Then $r = \|\mathbf q - \mathbf p\|$, $\theta$ is the angle between $\mathbf q-\mathbf p$ and the $x$-axis, $\overline{r}(x,y)$ is the average radius $$\overline{r}(x,y)=\frac1{2\pi}\oint_{\mathbf q\in\mathcal C}\|\mathbf q-\mathbf p\|\,\mathrm d\theta.$$

and $\mathbf{p}$ maximize is the average of points maximizing are the points maximizing $\overline{r}$.

(Conveniently, this integral can also be computed for non-star-shaped curves; for a ray that meets the curve multiple times, it amounts to taking the total length of all segments that lie in the interior of the curve.)

Note that "this center property" is not the centroid. This can be shown in Mathematica (thanks to @Rahul)

The center is computed using discretization, Euclidean Distance and Sums.

curve = DiscretizeRegion[
  ImplicitRegion[
   S1[x, y] == 1, {{x, -3, 3}, {y, -4, 4}}], {{-3, 3}, {-4, 4}}, 
  AccuracyGoal -> 8]
q = MeshCoordinates[curve];
edges = First /@ MeshCells[curve, 1];
signedAngle[a_, b_] := Arg[(Complex @@ a)/(Complex @@ b)]
avgRadius[p_] := 
 1/(2 \[Pi]) Abs[Sum[Module[{q1, q2, r, d\[Theta]}, q1 = q[[First@e]];
     q2 = q[[Last@e]];
     r = EuclideanDistance[p, (q1 + q2)/2];(*midpoint approximation*)
     d\[Theta] = signedAngle[q1 - p, q2 - p];
     r d\[Theta]], {e, edges}]]
s = FindMaximum[avgRadius[{x, y}], {{x, 0}, {y, 0}}]

The centroid, which is well-known, can be easily computed using RegionCentroid 

J = RegionCentroid[
  DiscretizeRegion[
   ImplicitRegion[
    S1[x, y] == 1, {{x, -3, 3}, {y, -4, 4}}], {{-3, 3}, {-3, 3}}, 
   AccuracyGoal -> 8]]

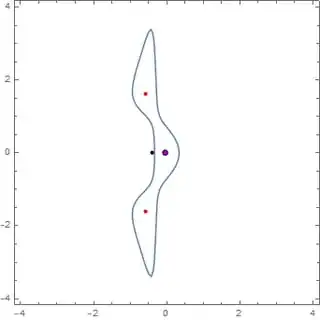
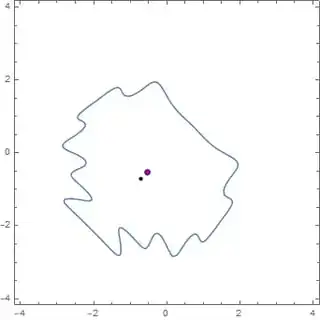
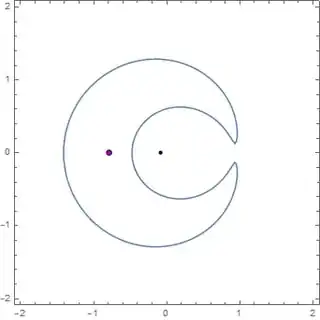
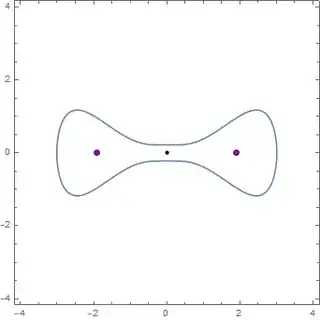
I plotted $\mathbf{p}$, the maximas and the curve. The red dots reprsent the maximas, the blue dot repesents $\mathbf{p}$ and the black dot represents the centroid.

Show[ContourPlot[S1[x, y] == 1, {x, -4, 4}, {y, -4, 4}], 
 Graphics[{PointSize {Medium}, Blue, 
   Point[{x /. s[[2, 1]],  y /. s[[2, 2]]}]}], 
 Graphics[{PointSize {Medium}, Black, Point[{J[[1]], J[[2]]}]}]]

Here are some examples. I'm unable to solve my center in closed form.

$2x^2+2y^2+7y\sin{(xy)} + 7x\sin{(x)}=1$

Center1

$x^2 + x + y^2 + y + \sin(xy) + \sin(3xy)=4$

Center2

$(x^2+y^2-1)^2+.415x=.4$

Center3

$81y^2-x^4\left(9-x^2\right)=4$

Centers4

Pros and Cons of "The Center Property"

Pros:

  • Its reasonable
  • Close to the centroid if star-shaped
  • Within the boundary of the curve (if star-shaped)
  • Leads to interesting problems regarding the maxima of $\overline{r}(x,y)$

Cons:

  • Tedious to solve mathematically. Rarely has a closed form. Rarely has an elegant solution.
  • If curve is 2-d, even if $\overline{r}$ is exact, you must find the maxima of $\overline{r}(x,y)$ in 3-d Coordinates
  • If the curve is 3-d, you must find the maxima of $\overline{r}(x,y,z)$ in 4-d Coordinates.

Unproven Assumptions

  1. If the curve is star-shaped and closed $\overline{r}$ has one maxima
  2. If the curve is star-shaped and closed, $\mathbf{p}$ stays inside.
  3. If the curve is star-shaped and closed one $\mathbf{p}$ exists
  4. The proximity of the centroid and "the property" determines the even distribution of the closed shape.

In conclusion, I have the following questions?

Are there other centers excluding the centroid?

Is "my property" new? Can it be applied in theoretical mathematics? Applied math? Physics?

Lastly, if you are intereseted, use this for research. I'm too young to "analyze".

Arbuja
  • 1
  • 3
    So your center is a point maximizing the integral? I wonder if it is unique. Could there be more than one point maximizing the integral? – Cheerful Parsnip Dec 29 '17 at 03:12
  • I'm confused - you define an integral, but you never define what your center is, as far as I can see (without going into the code)? – Milo Brandt Dec 29 '17 at 04:08
  • How do I decide what $\mathbf p$ to use, and/or does it matter? – Calvin Khor Dec 29 '17 at 04:20
  • An interesting question here, to start with: what is it in a triangle? –  Dec 29 '17 at 04:34
  • @GrumpyParsnip Yes, the center maximizes the integral. Sorry for not mentioning, I didn't get much sleep..... – Arbuja Dec 29 '17 at 11:52
  • @GrumpyParsnip For non-star shapes, I'm sure it is unique but what for non-star shapes I'm unsure. (However, in my post what I meant by "unique" is that center is "different" from the centers known). – Arbuja Dec 29 '17 at 11:55
  • @MiloBrandt The center maximizes the integral. I didn't get much sleep. – Arbuja Dec 29 '17 at 11:56
  • @CalvinKhor The $\mathbf{p}$ that maximizes the integral is the center. – Arbuja Dec 29 '17 at 11:57
  • 3
    Just for reference, your integral can be written only using the parametrization $\alpha : I \to \mathbb{R}^2$ of the curve $\mathcal{C}$: $$\oint_{\mathcal{C}} | \mathrm{p} - \mathrm{q} | , d\theta = \int_{I} \frac{|\alpha'(t) \times (\alpha(t) - \mathrm{p})|}{|\alpha(t)-\mathrm{p}|} , dt $$ Here, $\times$ is understood as the cross product when 2d vectors are regarded as 3d vectors on the $xy$-plane. – Sangchul Lee Dec 29 '17 at 12:33
  • @user8734617 I checked, and I am sure it is the centroid. However, I could not determine this in closed form. – Arbuja Dec 29 '17 at 16:53
  • @Arbuja I think the uniqueness question is an interesting one for a research project. – Cheerful Parsnip Dec 30 '17 at 03:21
  • Maybe helpful : Is there an easy way to determine a point from its barycentric coordinates geometrically? . – Han de Bruijn Jan 02 '18 at 12:43
  • @SangchulLee You cant use any parametrization. The parametrization must be based off a rotating line at a point, increasing at an increment, to give the correct average radius at that point. For example, the paramteric equation $(2\cos{(t)},3\sin(t))$ of the ellipse won't return the correct average radius as a parametric curve derived from converting the ellipse to a polar equation. – Arbuja Jan 03 '18 at 01:15
  • You can always represent both $\mathrm{q}$ and $\theta$ in terms of arbitrary regular parametrization $\alpha$ of $\mathcal{C}$, and the result from this reparametrization is the above expression I explained. (Actually, the expression above is true only when $\mathcal{C}$ is star-shaped around $\mathrm{p}$. We need a slight generalization which true for any nice $\mathcal{C}$.) – Sangchul Lee Jan 03 '18 at 01:46
  • 1
    For a simple explanation, consider the polar coordinates (centered at $\mathrm{p}$) and notice that $r=|\mathrm{q}-\mathrm{p}|$ and $\theta$ satisfies $ds^2=(rd\theta)^2+dr^2$. So your integral can be written as$$\oint_{\mathcal{C}}r,d\theta=\oint_{\mathcal{C}}\sqrt{ds^2-dr^2}=\oint_{\mathcal{C}}\sqrt{\left(\frac{ds}{dt}\right)^2-\left(\frac{dr}{dt}\right)^2},dt.$$Now simplifying the integral yields the above expression. – Sangchul Lee Jan 03 '18 at 01:47

1 Answers1

5

I'm sorry that this answer is quite terse. I don't have time to explain it in more detail, but I've marked it community wiki in case someone else is interested in expanding it (and adding some diagrams, which would help).

Let $\mathbf x$ be a point on the curve, $\mathbf r = \mathbf x-\mathbf p$ be the vector from $\mathbf p$ to $\mathbf x$, and $\phi$ be the angle between $\mathbf r$ and the curve normal $\mathbf n$ (i.e. the unit vector perpendicular to the tangent). One can show by drawing a small diagram that $$\|\mathbf r\|\mathrm d\theta = \mathrm d\ell\cos\phi = \left(\frac{\mathbf r}{\|\mathbf r\|}\cdot\mathbf n\right)\mathrm d\ell.$$ Therefore, the integral is equal to $$\bar r(\mathbf p) = \oint \|\mathbf r\|\,\mathrm d\theta = \oint \frac{\mathbf r}{\|\mathbf r\|}\cdot\mathbf n\,\mathrm d\ell,$$ and by the divergence theorem this equals $$\bar r(\mathbf p) = \iint\left(\nabla\cdot\frac{\mathbf r}{\|\mathbf r\|}\right)\mathrm dA = \iint\frac1{\|\mathbf r\|}\,\mathrm dA$$ where the integral is taken over the area enclosed by the curve. In other words, $\bar r(\mathbf p)$ is the convolution of the indicator function of the area inside the curve with the kernel $1/\|\mathbf r\|$.

This fact makes it easy to construct a counterexample to assumption 1: Consider a dumbbell-shaped curve, enclosing two unit disks centered at $(-2,0)$ and $(2,0)$ connected by a thin path. One can verify numerically that there are two maxima, located in the interior of the two disks. It should also be possible to construct a counterexample to assumption 2 by considering a single disk with a long thin notch cut out of it, so that the center is inside the notch and thus outside the curve.

  • Does this mean "my center" is not a center since more than one absolute maximum exists? – Arbuja Dec 31 '17 at 12:36
  • However, two disks are divided into "two parts". If we take the average of $\mathbf{P}$ of the first disk and $\mathbf{P}$ of the second disk we get $(0,0)$ which is reasonable. – Arbuja Dec 31 '17 at 14:49
  • 2
    (1) You could say that. Or more precisely, the center is not well-defined. (2) I'm not talking about two disks separately, which would have two boundary curves. I mean a single dumbbell-like shape that is the union of the two unit disks and the rectangle with vertices $(\pm2,\pm0.1)$. Mathematically it only has one "part" (i.e. one connected component). –  Dec 31 '17 at 15:50
  • What if I took the average of the two maximas? I'm unable to discretize rectangular shapes, so I need your help with the coding. – Arbuja Dec 31 '17 at 17:01
  • What if we modified the definition for non-star shaped curves so that a ray meeting the curve multiple times can be outside the interior as long as it meets the boundary? – Arbuja Jan 07 '18 at 16:19
  • This means if a ray, emanating from point $\mathbf{p}$, toughes a non-star curve at $\mathbf{q_1}$ and $\mathbf{q_2}$, then we take $||\mathbf{q_1}-\mathbf{p}||+||\mathbf{q_2}-\mathbf{p}||$ regardless if the ray $\mathbf{p}\mathbf{q_2}$ is partially outside the interior. – Arbuja Jan 07 '18 at 16:24