$\newcommand{\Log}{\operatorname{Log}}$First set $x=2\arctan(t)$ so that:
\begin{align}
I:=\int^{\pi/4}_0 \ln^2\left(\tan^2\left(\frac x 2\right)\right)\,dx=8\int^1_0 \frac{\ln^2(t)}{1+t^2}\, dt
\end{align}
Now we set $t=\frac{1}{u}$ so that:
\begin{align}
I=-8\int^1_\infty \frac{\ln^2(u)}{1+u^2}\,du = 8\int^\infty_1 \frac{\ln^2(u)}{1+u^2}\,du
\end{align}
Putting these things together yields:
\begin{align}
I = 4 \int^\infty_0 \frac{\ln^2(u)}{1+u^2}\,du
\end{align}
Now let me be stubborn and integrate a slightly different thing, namely:
\begin{align}
\int_{K_R} \frac{\Log^3(-z)}{1+z^2}\,dz
\end{align}
Where $\Log(\cdot)$ is the Principal Value of the logarithm and $K_R$ is the following contour consisting of $C_R$, $C_R^+$ and $C_R^-$ that can be seen in the picture below.
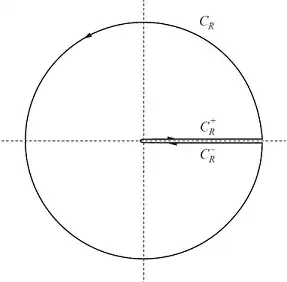
Let $R>1$, by The Residue Theorem we have:
\begin{align}
\int_{K_R} \frac{\Log^3(-z)}{1+z^2}\,dz = 2\pi i \left(\frac{\Log^3(-i)}{2i} +\frac{\Log^3(i)}{-2i}\right)=\frac{i\pi^4}{4}
\end{align}
That means:
\begin{align}
\int_{C_R} + \int_{C_R^-} +\int_{C_R^+} \frac{\Log^3(-z)}{1+z^2}\,dz = \frac{i\pi^4}{4}
\end{align}
When $R\to \infty$ we have the contribution from $C_R$ goes to zero ($\star$). On $C_R^+$ we have:
\begin{align}
\lim_{R\to\infty}\int_{C_R^+}\frac{\Log^3(-z)}{1+z^2}\,dz = \int^\infty_0 \frac{\ln^3(t)-3i\pi\ln^2(t)-3\pi^2\ln(t)+i\pi^3}{1+t^2}\,dt
\end{align}
On $C_R^-$ we have:
\begin{align}
\lim_{R\to\infty}\int_{C_R^-}\frac{\Log^3(-z)}{1+z^2}\,dz = -\int^\infty_0 \frac{\ln^3(t)+3i\pi\ln^2(t)-3\pi^2\ln(t)-i\pi^3}{1+t^2}\,dt
\end{align}
Now you understand why I was being stubborn because putting these things together yields something that looks like $I$, namely:
\begin{align}
\int^\infty_0 \frac{-6i\pi\ln^2(t)+2i\pi^3}{1+t^2}\,dt =\frac{i\pi^4}{4}
\end{align}
Hence:
\begin{align}
-6\int^\infty_0 \frac{\ln^2(t)}{1+t^2} \,dt =\frac{\pi^3}{4}-2\pi^2\int^\infty_0 \frac{1}{1+t^2}\,dt
\end{align}
On the RHS we have a popular integral which evaluates to $\pi/2$ (how?) so we get:
\begin{align}
-6\int^\infty_0 \frac{\ln^2(t)}{1+t^2}\,dt = -\frac{3\pi^3}{4}
\end{align}
That means:
\begin{align}
\int^\infty_0 \frac{\ln^2(t)}{1+t^2}\,dt = \frac{\pi^3}{8}
\end{align}
So finally:
\begin{align}
\int^{\pi/4}_0 \ln^2\left(\tan^2\left(\frac x 2\right)\right)\,dx = 4\int^\infty_0 \frac{\ln^2(t)}{1+t^2}\,dt = \frac{\pi^3}{2}
\end{align}
($\star$) We actually have some small part of a circle with radius $\epsilon$ in the origin, but that circle also have no contribution when $\epsilon\to 0$ using the ML-lemma.
