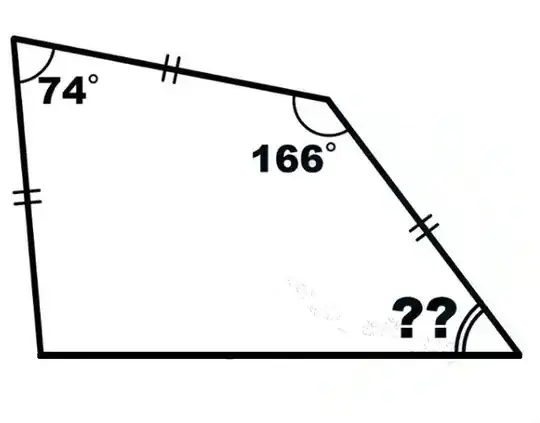
I was working on this problem. I tried to draw ${AC}$, ${BD}$ as isosceles triangle and divide into cases to find the missing angle $??$, but I got stuck. Can someone help me please or give me a clue?
- 145,942
- 24,922
-
The smallest triangle on CD is isosceles, by the sine rule on triangles BCD and ACD. – Empy2 Dec 13 '17 at 07:54
-
I hate to sound like everyone's math teacher, but this is definitely a case where making a reasonable scale drawing will guide your intuition for the formal proof. – jwg Dec 14 '17 at 11:33
5 Answers
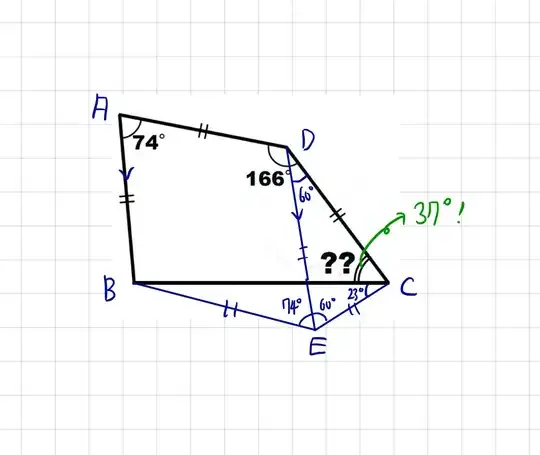
Though Robert gave a great solution, I post another solution with a picture. Draw a line $\overline{DE}$ parallel to $\overline{AB}$, toward $\overline{BC}$. Then $\triangle DEC$ becomes an equilateral triangle and $\square ABED$ becomes a parallelogram, and in turn rhombus which makes $\triangle BEC$ be isosceles triangle. Thus we have $\angle BED = 74^\circ$,$\angle DEC=60^\circ$, and $\angle BCE = 23^\circ$. Therefore, we have $\angle DCE = 60^\circ - 23^\circ = 37^\circ$.
- 464
There is a point $E$ along $DC$ such that $\triangle ABE$ is equilateral (why? See my P.S.). Therefore $$\hat{ADC}=\frac{1}{2}(180^\circ-(74^\circ-60^\circ))=83^\circ\quad\text{and}\quad \hat{BCD}=\frac{1}{2}(180^\circ-(166^\circ-60^\circ))=37^\circ.$$
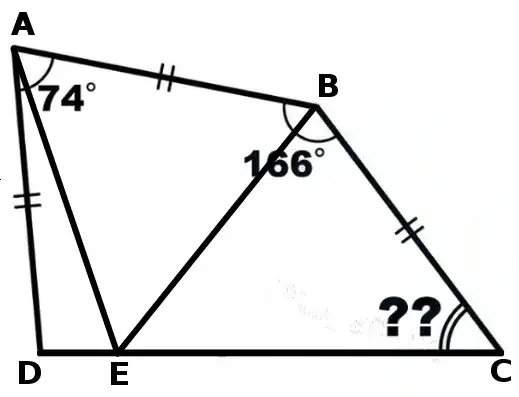
Note that your picture is misleading because the angle at $D$ should be acute!
P.S. Go backwards. Start form the equilateral triangle $\triangle ABE$. Then draw externally the isosceles triangle $\triangle AED$ with an angle at $A$ of $14^\circ$, and the isosceles triangle $\triangle BEC$ with an angle at $B$ of $106^\circ$. Then $D$, $E$ and $C$ are on the same line because $$\hat{AED}+\hat{AEB}+\hat{BEC}=83^\circ+60^\circ+37^\circ=180^\circ.$$
- 145,942
-
1
-
@Robert I was wrong earlier. If angle ADC is less than 90 (which is the case here) then you can be correct. But how did you know that before hand? – jonsno Dec 13 '17 at 08:24
-
I did think you went backwards. if that's what you did. A nice solution indeed! – jonsno Dec 13 '17 at 08:48
-
@RobertZ :Would you please ,make details more clear ? Possible draw a figure ? (thanks again) – Khosrotash Dec 13 '17 at 10:01
-
@Khosrotash I I did my best. Note that in your picture the angle at D should be acute! $\triangle ADE$ is isosceles!! – Robert Z Dec 13 '17 at 10:36
-
-
Although the first sentence seems to be right, the combination of the surprising assertion and the backwards justification in the PS certainly don't make anything easier to understand than a more straightforward angle-chasing proof. – jwg Dec 13 '17 at 11:42
-
@jwg Actually the first sentence SEEMS TO BE WRONG (see comments and 2 downvotes), but finally it IS RIGHT!! – Robert Z Dec 13 '17 at 11:56
-
@RobertZ No I didn't downvote. I don't generally downvote, I leave comment instead. – Jaideep Khare Dec 13 '17 at 12:46
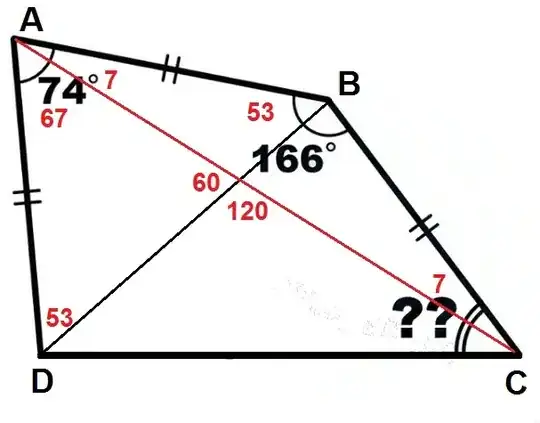
Only thing to realise here was that $\sin(\pi - x) = \sin (x)$. So $\sin DAC = \sin (\pi - DBC) = \sin DBC$. Also $AD = AB = BC$
Then we apply sine rule on $DAC$ and $DBC$ triangles.
$$\frac{\sin DCA}{ AD} = \frac{\sin DAC}{DC}$$ and $$\frac{\sin CDB}{ BC} = \frac{\sin DBC}{DC}$$
So we get angle $\angle DCA = \angle CDB = 30$ (seen from triangle $DOC$ where centre point is $O$) or the required angle as $37 ^\circ$.
- 7,521
This is somehow an ugly approach. Nevertheless, you can calculate $BD$ using the law of cosines. Then apply the law of cosines in $BDC$ to calculate $DC$ and use the law of sines to get the unknown angle.
- 9,245
-
2
-
5@RosieF you may even get some interesting results, such as :)) $$\sin 37=\sin 67 \sqrt{\frac{1 - \sin 16}{3/2-\sin 16+\sqrt{2}\sin 23\sqrt{1-\sin 16}}}$$ – polfosol Dec 13 '17 at 10:42
-
1
-
@polfosol:From where ? you can get this formula ...can you elaborate more please ? – Khosrotash Dec 15 '17 at 08:46
-
1@Khosrotash I am on mobile, so I should make it as brief as possible. If you follow the procedure I described in my answer, you will see that
sin BCD / sin DBC = BD / CDand sinceDBC =67, BCD =37we end up with that formula. – polfosol Dec 15 '17 at 18:33
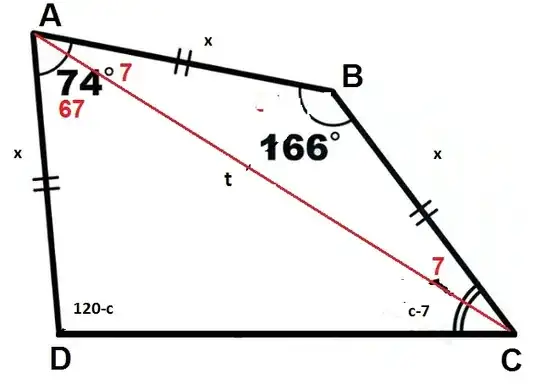
$$AB=AD=BC=x,AC=t\\t^2=x^2+x^2-2x^2\cos166\\\to t^2=2x^2(1-\cos166)=2x^2(2\sin^2(83))=4x^2\cos^2(7)\\t=2x\cos 7$$so $$\frac{t}{\sin(120-c)}=\frac{x}{sin(c-7)}\\\frac{2x\cos 7}{\sin(120-c)}=\frac{x}{sin(c-7)}\\2\sin(c-7)\cos 7=\cos(30-c)$$using product to sum formula $$\sin(c-14)+\sin c=\cos(30-c)\\ \sin 30 \cos c+ \cos 30 \sin c+\sin c=\cos 30 \cos c + \sin30 \sin c\\\sin c(1-\frac 12 +\cos 14)=\cos c(\cos 30+\sin14)\\\tan c=\frac{\cos 30+\sin 14}{\frac12+\cos 14}=\frac{\sin 60+\sin 14}{\cos 60+\cos 14}=\frac{2\sin37 \cos 23}{2\cos37 \cos 23}=\tan(37)$$finally $$\tan(c)=\tan(37) \to c=37$$
- 24,922