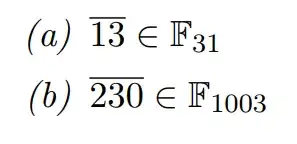1

In the following task I have been instructed to "Calculate the inverse of the following elements".

Searching for what the vinculum could mean here as well as what the notation of F could mean in a list of mathematical symbols has been fruitless in aiding my understanding of the assigned task.

I am hoping someone with a more trained mathematical eye can tell me what is being asked here.

Exercise tasks a and b

Note: It is possible that the Tags are misnomers, I have tried to make an educated guess based on what subjects we are doing at Uni. Apologies in advance.

Arkady
  • 9,315
Jackie
  • 705
  • 5
  • 17

1 Answers1

3

The overline is showing that the value is a representative member of the congruence class (or residue class).

$\Bbb F_n$ is referring to the finite field for modular arithmetic on that prime $n$. In general modular arithmetic modulo $n$ is on the ring $\Bbb Z/n\Bbb Z$ but for $n$ prime this is a field.

An inverse of $a \bmod m$ is looking a number (residue) $k$ such that $ak\equiv 1 \bmod m$. Then $k$ is the inverse of $a \bmod m$, which may be written as $k\equiv a^{-1} \bmod m$

For example, the inverse of $5 \bmod 17$ is $7$ because $5\cdot 7=35\equiv 1 \bmod 17$.

In general to find the modular inverse you can use the extended Euclidean algorithm. Some more discussion on finding these at this question.

Joffan
  • 39,627
  • 1
    Thanks, I was able to utilize this method to calculate the solutions a) 12 and b) 580 respectively.

    I have not yet grasped the concept of a field, so i will inform myself on this topic next.

     – Jackie Dec 07 '17 at 00:41
  • It's probably easier to simply work at modular arithmetic and then later - when you encounter fields in a more generic sense - you will have an example to refer to. – Joffan Dec 07 '17 at 01:10