1

This question is nearly identical - I would have commented there, but I suppose the post is too old. I would like to extend that scenario slightly.

Using Tpofofn's diagram - vector (a,b) is clockwise from vector (c,d) - and hence the determinant (a,b) x (c,d) is positive.

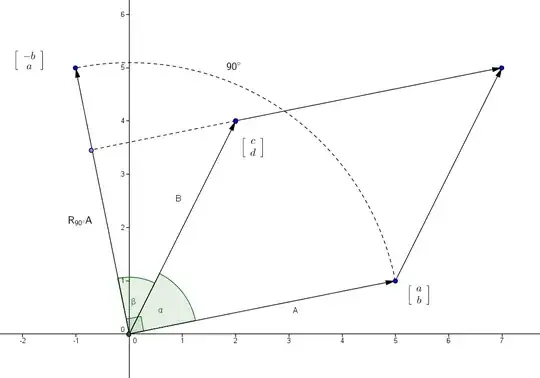
Determinant Figure

Consider a scenario where the two vectors are moving towards each other. The parallelogram is becoming stretched as the two vectors approach each other. Finally, the two points are colinear and hence the determinant is 0.

Here's my question - When the two lines cross, the determinant (a,b) x (c,d) is now negative. But why? What does the parallelogram look like as the two vectors continue to move away from each other?

Community
  • 1
Jmoney38
  • 111
  • 2
  • 1
    The fact is that the cross product orientation is changed. The area is the same if you take its absolute value, otherwise you have to take car of the direction of the cross product. – Sigur Dec 09 '12 at 00:18
  • Ahh!! That makes sense!! I was too focused on the area of the parallelogram as a side-effect, and didn't even think about the cross product being a vector... Right hand rule, etc... Thank you. – Jmoney38 Dec 09 '12 at 00:40
  • You are welcome. – Sigur Dec 09 '12 at 00:46

0 Answers0