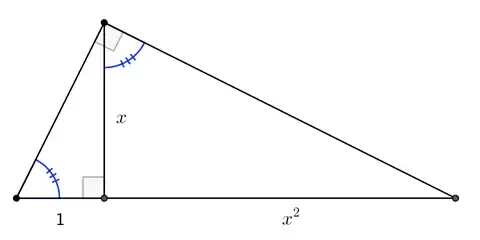
The author is trying to prove it is impossible to square a circle of radius $1$ under the assumption that $\pi$ is transcendental. Even with this assumption, the author explains that if the circle can be squared, then we could draw a line with distance $\pi^{1/2}$. Everything good at the moment. Then he claims that, if such construction is possible, we could also draw a line of distance $\pi$, and that the proof would, under the stated assumption, be complete.
The thing I don't get is how, from a line with distance $\pi^{1/2}$, we could create a line with distance $\pi$.