35

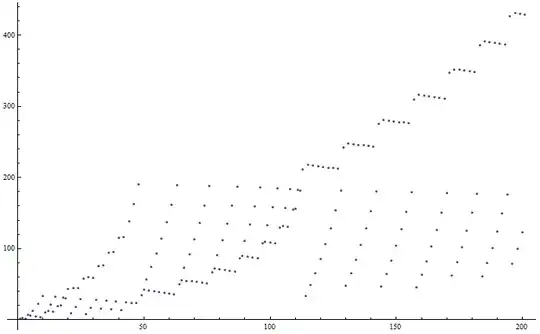
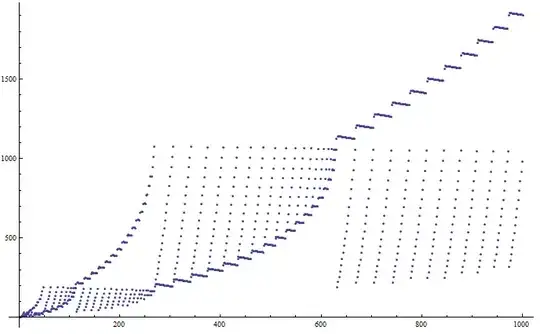
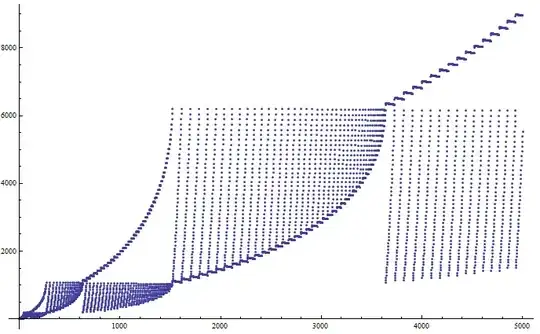
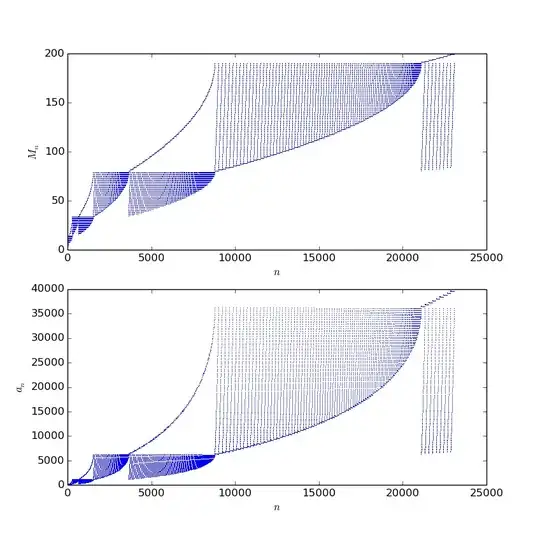
An infinite sequence of pairwise distinct numbers $a_1, a_2, a_3, ...$ is defined thus: $a_n$ is the smallest positive integer number such that $\sqrt{a_n+\sqrt{a_{n-1}+...+\sqrt{a_1}}}$ is positive integer.

Prove that the sequence $ a_1, a_2, a_3, ... $ contains all positive integers numbers.

My work:

Let $a_1=1$. Then $\sqrt{a_2+1}$ is positive integer and $a_2$ is the smallest positive integer then $a_2=3$.

Then $\sqrt{a_3+2}$ is positive integer and $a_3$ is the smallest positive integer then $a_3=2$.

Then $\sqrt{a_4+\sqrt{a_3+\sqrt{a_{2}+\sqrt{a_1}}}}=\sqrt{a_4+2}$ is positive integer and $a_4$ is the smallest positive integer and $a_4\not=a_1,a_2,a_3$ then $a_4=7$.

Community
  • 1
Roman83
  • 17,884
  • 3
  • 26
  • 70

4 Answers4

26

(not an answer, only meant to share my astonishment)

Look at it, guys! Just freaking look at it!

First 50 terms: 1, 3, 2, 7, 6, 13, 5, 22, 4, 33, 10, 12, 21, 11, 32, 19, 20, 31, 30, 43, 9, 45, 18, 44, 29, 58, 8, 60, 17, 59, 28, 75, 16, 76, 27, 94, 15, 95, 26, 115, 14, 116, 25, 138, 24, 163, 23, 190, 35, 42.

First 200 terms: First 200 terms

First 1000 terms: First 1000 terms

First 5000 terms: First 5000 terms

My first guess was that the thing is chaotic, and we won't ever be able to prove a thing. Now I've changed my mind.

Ivan Neretin
  • 12,835
22

Consider the sequence of square roots $s_n$, where $s_n=\sqrt{a_n+s_{n-1}}$. This sequence starts out $1,2,2,3,3,4,3,5,3,\ldots$. If we can show that every positive integer occurs at least once in this sequence, then we can conclude that every positive integer occurs (exactly once) in the sequence of $a_n$'s: each integer $k$ must occur among the $a_n$'s no later than the first time $s_{n-1}=k^2-k$.

Observe first that the sequence of $s_n$'s cannot recycle a finite set of values infinitely often, since $a_n=s_n^2-s_{n-1}$ must not repeat. So there must be an infinite number of "new" values in the sequence.

To show that every positive integer occurs in the sequence of $s_n$'s, it suffices to show that each "new" value in the sequence is precisely one more than the previous "new" value -- e.g., $7$ won't occur as an $s_n$ until after $6$ has occurred. To prove this, note that if $s_1,s_2,\ldots,s_{n-1}\le k$, then $a_1,a_2,\ldots,a_{n-1}\lt k^2$ (since $a_j=s_j^2-s_{j-1}$). Since $(k+1)^2-s_{n-1}\ge k^2+k-1\gt a_j$ for all $j\lt n$ and $a_n$ is the smallest positive integer (not already in the sequence) for which $a_n+s_{n-1}$ is a square, we must have $s_n\le k+1$.

Barry Cipra
  • 79,832
  • 1
    "If we can show that every positive integer occurs at least once in this sequence, then we can conclude that every positive integer occurs (exactly once) in the sequence of $a_n$'s" I'm not convinced by your argument proving this, can you elaborate? – orlp Oct 12 '17 at 17:41
  • 1
    @orlp, if $s_{n-1}=k^2-k$, then $a=k$ is the smallest integer for which $a+s_{n-1}$ is a perfect square, so the only reason we wouldn't let $a_n=k$ is if $k$ has already appeared in the sequence of $a_j$'s. – Barry Cipra Oct 12 '17 at 17:46
  • Yes, you've made that much clear, but it's not at all obvious to me that if $s_{n-1} = k^2 - k$ that $k$ takes on all integer values as the sequence progresses. – orlp Oct 12 '17 at 17:48
  • @orlp, It's not $k^2-k$ that takes on all integer values, it's the sequence $s_n$ that takes on all integer values (which is proved in the final two paragraphs). – Barry Cipra Oct 12 '17 at 17:51
  • @orlp, if $k$ (greater than $1$) is a positive integer, then $k^2-k$ is also a positive integer. If the sequence of square roots takes on all positive integers (which, as I said, is proved in the final two paragraphs), then it somewhere takes on the value $k^2-k$. Thus there is an $n$ such that $s_{n-1}=k^2-k$. – Barry Cipra Oct 12 '17 at 18:00
4

Not an answer but some additional graphics to @Ivan Neterin's answer (not an answer).

I was wondered not about $a_n$'s but those integers $$ M_n = \sqrt{a_n + \sqrt{a_{n-1} + ...}}$$ And what I find? BOOM. Unexpected (at least for me). enter image description here I do not know if it is some visual noise or not but you can notice kind of parabolic curves on pictures. Interesting what is their nature. enter image description here

LRDPRDX
  • 1,288
4

It seems to me, from looking at the graphs in Ivan Neretin's answer, that one change of phase is indicated by $a_i=a_{i-1}-1$. The change of phase the other way could be defined by the highest $a_i$ preceding a phase-change of the first kind. I realise that there are alternative definitions of when exactly the phase changes. But with the above definitions, the changes of the first kind are at $i=3, 5, 19, 112, 630, 3637, 21101, 122766, 714992, 4165987, 24278023,\dots$, with $a_i=2, 6, 30, 182, 1056, 6162, 35910, 209306, 1219920, 7110222, 41441406,\dots$. In each case, the preceding high points were at $i=2, 4, 10, 48, 269, 1521, 8780, 50942, 296383, 1726143, 10057582,\dots$ with $a_i=3, 7, 33, 190, 1075, 6208, 36021, 209574, 1220567, 7111784, 41445177,\dots$. With each of these four sequences, the ratio of term to preceding term seems to converge to the value $3+2\sqrt2\sim5.82842712474619$ which is the limit of the term-ratio of the recurrence $b_n=6b_{n-1}-b_{n-2}$. (The term-ratios of the above sequence $a_i=2, 6,\dots$ converge somewhat more quickly than those of the other sequences above.)

Rosie F
  • 2,913
  • 2
    Convolving that sequence [2, 6, 30, ...] with [1 -6 0 6 -1] -- i.e., multiplying the generating function by $(x^2-6x+1)(x^2-1)$ -- appears to give [-2,0,0,0,0, ...]. The g.f. of the sequence accordingly seems to be $\frac{2(1-3x-3x^2+7x^3-x^4)}{(1-6x+x^2)(1-x^2)}$. This is all purely empirical, and furthermore I haven't checked any coefficients beyond the ones in the answer above. – Gareth McCaughan May 12 '19 at 20:50