Backed up by direct experience and the following reference:
H. de Bruijn and W. Zijl; Numerical Simulation of the Shell-Side Flow and Temperature Distribution in Heat Exchangers;
Handbook of Heat and Mass Transfer; chapter 27; Volume 1: Heat Transfer Operations; Nicholas P. Cheremisinoff, Editor;
Gulf Publishing Company (1986).
Focusing on both theoretical and numerical aspects of PDEs:
Summary
Problem description: how to describe the complex transport phenomena in the flow around the tubes of a shell-and-tube
heat exchanger, such as the one depicted below.
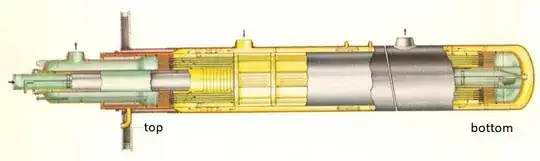
In order to describe the shell-side flow and temperature distribution, investigators have
attempted the so-called
fluid-tube continuum approach. The basic idea of the method is: setting
up partial differential equations for a kind of
porous medium.
Wrap a control-volume around a couple of tubes. Set up the energy balances for this volume. Let the volume become
"infinitesimally small", though still remaining larger than the distance between the tubes. Or throw away the integral
signs after applying Gauss theorems. Or whatever. Then the following set of Partial Differential Equations may be
inferred for Heat Exchange in a tube bundle:
$$
c.G_P \left[ u.\frac{\partial T_P}{\partial r} + v.\frac{\partial T_P}{\partial z} \right]
+ a.(T_P - T_S) = 0 \qquad \mbox{: shell side} \\
c.G_S.\frac{\partial T_S}{\partial z} +a.(T_S - T_P) = 0 \qquad \mbox{: tube side}
$$
Here: $c=$ heat capacity; $G=$ mass flow; $T=$ temperature; $(r,z)=$
cylinder coordinates; $(u,v)=$ normed velocities; $a=$ total heat
transfer coefficient; $P=$ primary; $S=$ secondary.
The boundary conditions should not be forgotten:
$$
T_P = T_{PL} \qquad \mbox{at the primary inlet (upper perforation)} \\
T_S = T_{S0} \qquad \mbox{at the secondary inlet (tube plate below)}
$$
One would think that what engineers really want is a realistic flow.
Unexpectedly perhaps, that's NOT what they really
want. With the apparatus I've been working on, what the engineers want
is the flow field, calculated in such a way that temperature stresses
cannot be worse in reality than they are in the calculations. We call
such calculations conservative. An insightful moment of thinking has
revealed that not a realistic flow simulation but rather an Ideal Flow
simulation has the desired properties:
Consequently, the (Partial Differential) equations for flow in a tube bundle may be
assumed to be those for incompressible and irrotational flow, in a cylindrically
symmetric geometry:
$$
\frac{\partial ru}{\partial r} + \frac{\partial rv}{\partial z} = 0
\qquad ; \qquad
\frac{\partial v}{\partial r} - \frac{\partial u}{\partial z} = 0
$$
Here: $u$ = horizontal velocity component, $v$ = vertical velocity component,
$r$ = horizontal radius, $z$ = vertical distance. With proper boundary conditions.
This completes the analytical description.
The numerical treatment of such systems of first order PDE's is quite another story; there exist visualizations of some results. And there are related references at Mathematics Stack Exchange:
