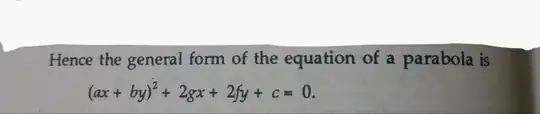How do I find details of a parabola from its general two-degree equation?

Question

This general equation in two-degree represents a parabola: $$(ax + by)^2 + 2gx + 2fy + c = 0$$

How do I find the following from this equation:

Vertex
Focus
Axis
Length of Latus Rectum
Co-ordinates of end points of Latus Rectum
Equation of Directrix

I know how to find these if a parabola has its axis parallel to either of the co-ordinate axes. But I don't know how to derive these from the general equation.

N.B.: w.r.t. a comment by @Vasya, I produce this picture from my book, where it says that the general form of the equation of a parabola is the above equation. The book gives the equation, but doesn't derive any of the above from the equation:

Hence the general form of the equation of a parabola is $$ (ax + by)^2 + 2gx + 2fy + c = 0. $$

enter image description here

This question gives the equation of a parabola with directrix $lx+my+n=0$ and focus $P(x_P,y_P)$ as $\frac{(lx+my+n)^2}{{l}^2+{m}^2}=(x-x_P)^2+(y-y_P)^2$. — Jan-Magnus Økland, Oct 04 '17 at 17:09
@Vasya please see the image. It might take a bit of time to load. — Wrichik Basu, Oct 04 '17 at 18:03
@Jan-MagnusØkland that shows that the equation of a parabola can have both $x^2$ and $y^2$ terms. — Wrichik Basu, Oct 04 '17 at 18:04
Yes, in $ax^2+2bxy+cy^2+2dx+2ey+f=0$, $b^2-ac$ just needs to vanish, see also wikipedia. — Jan-Magnus Økland, Oct 04 '17 at 18:11
Since you know how to find these values for an axis-aligned parabola, try finding a coordinate transformation that aligns the parabola. Hint: such a transformation will eliminate the cross-term $2axy$. You might also find some clues to finding these properties in the derivation of this general equation. — amd, Oct 04 '17 at 19:48
See Article $#359$ of https://archive.org/details/elementsofcoordi00loneuoft/page/332/mode/2up — lab bhattacharjee, Feb 02 '20 at 14:19

score 2 · Accepted Answer · answered Oct 05 '17 at 14:49

$y'=bx-ay$ is parallel to the directrix and $x'=ax+by$ parallel to the axis. This we can see from comparing to the form I mentioned in the comments. So let these be the new coordinates. The inverse is $x=\frac{ax'+by'}{a^2+b^2}$, $\frac{bx'-ay'}{a^2+b^2}$, transforming your equation into $$x'^2+2g\frac{ax'+by'}{a^2+b^2}+2f\frac{bx'-ay'}{a^2+b^2}+c=0,$$ solving for $y'$ we get $$y'=\frac{a^2+b^2}{2(fa-gb)}x'^2+\frac{ga+fb}{fa-gb}x'+c\frac{a^2+b^2}{2(fa-gb)}=Ax'^2+Bx'+C,$$ making (from the formulas given here) $x'=-\frac{B}{2A}$ or $ax+by=-\frac{ga+fb}{a^2+b^2}$ the axis and $y'=\frac{4AC-B^2-1}{4A}$ or $bx-ay=\frac{c(a^2+b^2)-g^2-f^2}{2(fa-gb)}$ the directrix. The semi latus rectum is $p=\frac1{2A}=\frac{fa-gb}{a^2+b^2}$. For the vertex and focus to undo the transformation we transform the point back. The vertex in the rotated coordinates is $(-\frac{B}{2A},\frac{4AC-B^2}{4A})$ making the vertex in the first coordinates $$(\frac12 \frac{-2 g a^3 f+g^2 a^2 b-2 f^2 b a^2+b c a^4+2 c a^2 b^3+c b^5-f^2 b^3}{(a^2+b^2)^2 (f a-g b)},-\frac12 \frac{-2 g^2 a b^2+f^2 b^2 a-2 f b^3 g+c a^5+2 c a^3 b^2+a c b^4-g^2 a^3}{(a^2+b^2)^2 (f a-g b)})$$ and the focus is $(-\frac{B}{2A},\frac{4AC-B^2+1}{4A})$, using the inverse transformation the focus is $$(\frac12 \frac{b c a^2-2 f a g+g^2 b+c b^3-f^2 b}{(a^2+b^2) (f a-g b)},-\frac12 \frac{c a^3+a f^2+a c b^2-g^2 a-2 f g b}{(a^2+b^2) (f a-g b)}).$$

How do I find details of a parabola from its general two-degree equation?

1 Answers1