-1

I have two normal distributions N(m1, s1) and N(m2, s2). I have two arrays A and B each of n elements, such that each array contain 1000 samples from each distribution. I have summary statistics of Array A and B such as max(A), max(B), mean(A), mean(B) and so on.

Array C consists of n elements and each element contains the results of a pairwise multiplication of array A and array B. How many samples do I have to take from C before I can get an estimate of the upper bound with a high degree of confidence (1 in 10^6)?

Realhermit
  • 101
  • Before calculations about estimates of the upper bound, what do you mean by "upper bound". These are normal distributions - so there isn't a max or upper bound on the values. – Mathemagical Sep 15 '17 at 00:11

1 Answers1

0

Speculative Comment. Certainly not an Answer.

If you have an actual application in mind, please give approximate means and standard deviations. Also, as @Mathematical has pointed out, normal distributions have no true maximum value, although there is little chance of a value more than four standard deviations above the mean. So instead of a maximum, would you be happy with a value not likely to be exceeded 1% of the time? 0.01% of the time?

Here is one possibly relevant item on this site. It probably doesn't answer your question, but it may help you sharpen up your description of what you're looking for. (And it has some interesting links.)

Suppose $X \sim \mathsf{Norm}(\mu_x=100,\sigma_x=15)$ and $Y \sim \mathsf{Norm}(\mu_y = 200,\sigma_y=10).$ Then a simple simulation will give you a pretty good idea of the distribution of $W = XY.$ You can easily get approximations of $\mu_w = E(W),\,\sigma_w = SD(W),$ and even the 99th quantile $q$ of $W,$ which is $q$ such that $P(W \le q) = 0.99.$ Note that $X$ and $Y$ are independent in this simulation. (This simulation used R statistical software, which is freeware, but many math and stat software packages could do something similar.)

m = 10^6;  x=rnorm(m, 100, 15);  y=rnorm(m, 200, 10)
w = x*y;  mean(w);  sd(w);  quantile(w, .99)
## 19997.9    # aprx E(W)
## 3170.564   # aprx SD(W)
##      99% 
## 27581.54   # aprx q with P(X < q) = .99

Below is a histogram of the simulated distribution. The vertical red line cuts 1% from its upper tail. The curve is the density curve of a normal distribution with a mean and SD suggested by the simulation.

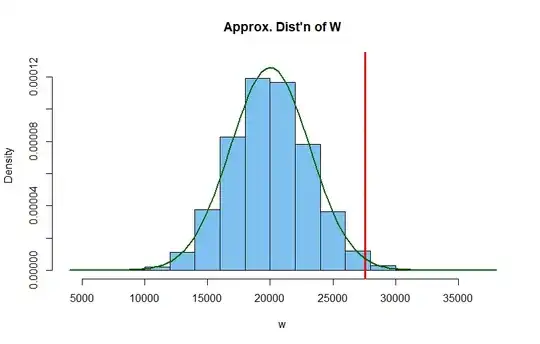
enter image description here

This simulation suggests that the product $W$ may be approximately normal, but in general, the product isn't normal. Sometimes not even close. Never make an important bet on the basis on one simulation.

Based on this arbitrarily chosen simulation, maybe you are interested in pursuing the theory behind your question, maybe you will want to try more simulations (matching an actual applied problem of interest), or maybe this will be the end of your interest. Particularly if you want to pursue the theory, please edit your question to be more specific about your goals.

BruceET
  • 51,500
  • I think where I may have erred is that the title of the question is a little different from the description of the question itself. I am actually less interested in the bounds on the product of two normal distributions, and more in the behavior of the population sampled from such distributions. Which means if I have some summary statistics of A and B, such as their mean, min and max - each a 1000 sample population, what can I infer about max(C)? – Realhermit Sep 15 '17 at 15:35