2

In his blog Terence Tao discusses the distance between powers of 2 and 3 and presents the following corollary:

Corollary 4 (Separation between powers of {2} and powers of {3})

  • For any positive integers {p, q} one has

    $$ \displaystyle |3^p - 2^q| \geq \frac{c}{q^C} 3^p$$

    for some effectively computable constants {c, C > 0} (which may be slightly different from those in Proposition 3).

What does he mean with "... effectively computable constants ... " ?

I've only a guess so far based on the inspection of the curve for $p$ and $q$ (=$N$ and $S$ in my usual notational style) using $p$ from the first hundred or so of the convergents of the continued fraction of $\log_2 (3)$ giving data for $p$ up to $1e175$ (only convergents where $2^q > 3^p$ are used).

From this I guess for instance $c=0.005$ and $C=1.01$. But those guesses might be much too crude.
I already presented an older guess in a MO-answer of mine but which seems even cruder.

So my question:

Q: How can one compute that constants?

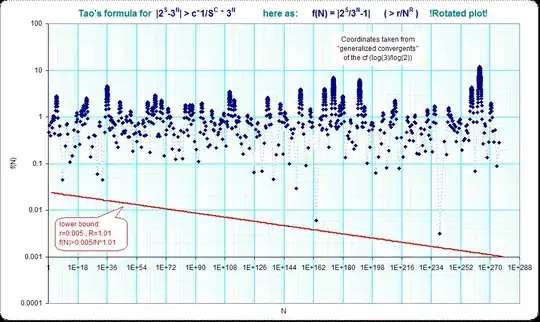
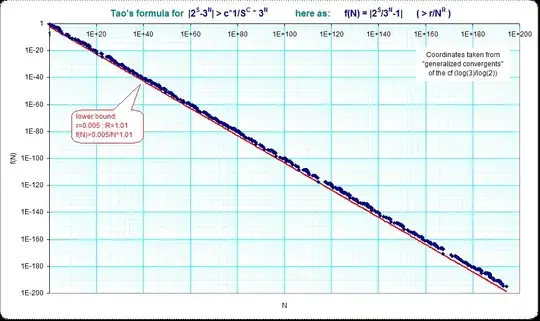
pictures making my guess. Used only that cases where $2^S > 3^N > 2^{S-1}$ that means also from the original convergents of the continued fractions only each second one.

Image for the whole tested interval:
pic1

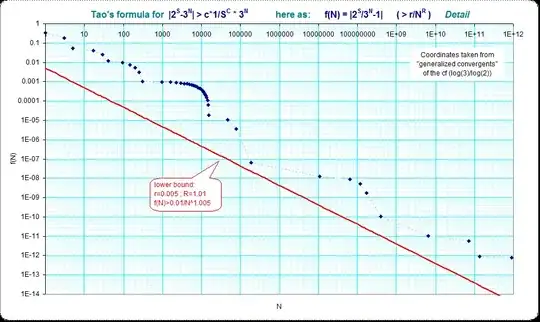
Detail for the smaller leading interval:
pic2

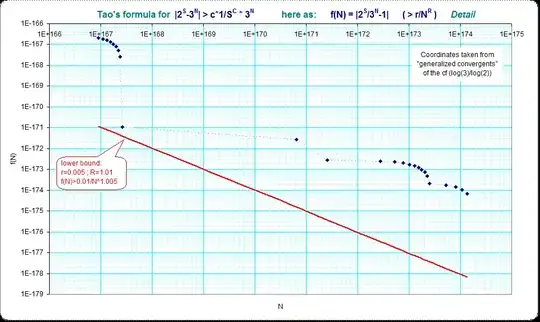
Detail for the smaller critical interval at $N \approx 1e166$:
pic3

Picture rotated to make comparision better visible. Note that the labeling of the axes are now no more correct, and the apparent numbers $N$ are scaled due to rotation (note: the logs of all values were rotated using $\cos(),\sin()$ by $45$ deg).
pic4

Gottfried Helms
  • 34,920
  • I'm assuming... by reading the proof of this Proposition 3 (or, rather, of Baker’s theorem of which it is a corollary), that presumably is proven in not only a constructive way, but by describing algorithmically how to obtain these constants. – Clement C. Sep 06 '17 at 12:09
  • @ClementC.- yes, this might be. But in any case: I'd like to see such a constructive computation or algorithm. I've come across such phrase "is effectively computable" frequently in the last weeks, but never found such computation been described - perhaps I'm missing some basic understanding here. – Gottfried Helms Sep 06 '17 at 12:58
  • Well, have you had a look at the proof in question? – Clement C. Sep 06 '17 at 13:00
  • @ClementC.:Hmm, I've read that blog-entry many times (not only this week) and never found any thing what would show me how I could actually do that "effective computation". Perhaps there's some blind spot on my side... – Gottfried Helms Sep 06 '17 at 13:07
  • Oh, I am talking about the proof of Baker’s theorem... I don't know it, but as far as I can see it's not in that blog post. – Clement C. Sep 06 '17 at 13:08
  • @clementc: ah, you suggest that such a description for the actual computation-method might be found in the paper which contains Baker's theorem and proof... – Gottfried Helms Sep 06 '17 at 13:10
  • Yes -- the blog post suggests the original proof is constructive and algorithmic. – Clement C. Sep 06 '17 at 13:11
  • @ClementC: ah well, I'll see... surprising that the values of that constants $c$ and $C$ are not very common and frequently documented - in sight of the frequent discussions of that problem of powers of 3 and 2. But I'll take your hint and try to see what I can find from that Baker's paper. Thanks for the hint so far. – Gottfried Helms Sep 06 '17 at 13:15
  • @GottfriedHelms in his blog does Terrence Tao discuss the relation between this and the Collatz conjecture? Or Mahler's 3/2 problem? – it's a hire car baby Sep 11 '17 at 09:06
  • @RobertFrost: yes, indeed he does (there are related two pages in his blog), but no explicte values for $c$ nor for $C$ is given – Gottfried Helms Sep 11 '17 at 09:08
  • @GottfriedHelms I have long thought this is the beating heart of the problem. I must see what he has written when I get a chance. There is a recent post on here which is related. – it's a hire car baby Sep 11 '17 at 09:15
  • @GottfriedHelms here's the post (with a good answer) which looks on the face of it related to yours but I haven't had chance to study your question in detail: https://math.stackexchange.com/questions/2398152/ – it's a hire car baby Sep 11 '17 at 10:29

1 Answers1

1

A method for computing the constants arising from linear forms of logarithms is clearly summarized here.

For the case where there are two logarithms, one can appeal to the results of Laurent, Mignotte, and Nesterenko for sharper constants (for references, see Exercise 4 from above, and see my related question).

Update 4/18/2018: One should also consider the work of Matveev (found in the references above) and G. Rhin ("Approximants de Padé et mesures effective s d'irrationalité").

rukhin
  • 195
  • 1
    Oh, thank you for the link. Unfortunately I haven't been able to go through this article of H-J- Evertsen a couple of years ago - I've got lost in space, so to say... Just recently I looked again at J. Simons papers on the disproof of the m-cycles in the Collatz-problem and took on to chew through the arguments around the result of G. Rhin - at least I seem to have understood this correctly (I showed my efforts in http://go.helms-net.de/math/collatz/Collatz_1cycledisproof.pdf for its open discussion of correctness) and so I think I have at least a glance of what is going on ... ;-) – Gottfried Helms Apr 18 '18 at 11:05
  • @GottfriedHelms Thanks for the references! – rukhin Apr 18 '18 at 18:20