Find $\lim\limits_{n \to \infty} \frac{\sqrt 1 + \sqrt 2 + \dots + \sqrt{n}}{n\sqrt{n}}$.

Question

$$\lim_{n \to \infty} \dfrac{\sqrt 1 + \sqrt 2 + \dots + \sqrt{n}}{n\sqrt{n}}$$

$$\lim_{n \to \infty} \dfrac{\sqrt 1 + \sqrt 2 + \dots + \sqrt{n}}{n\sqrt{n}} =\lim_{n\to \infty} \dfrac1{n}\sum^{n}_{k = 1} \sqrt{\dfrac k n} $$

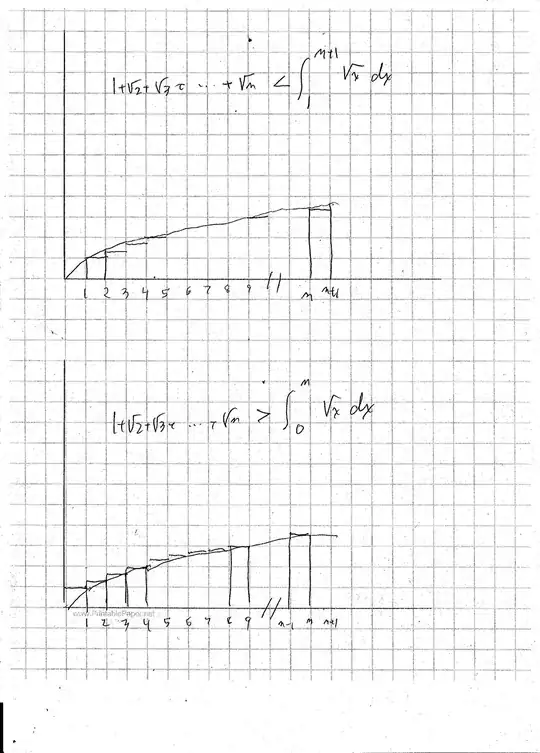
While searching this question I found, Turning infinite sum into integral.

Like in the accepted answer I first compared my series to LRAM,

$$\int_a^b f(x)\,dx=\lim_{n\to\infty}\frac 1n\sum_{i=1}^n f\left(a+\frac{b-a}n i \right)$$

I got $a = 0$, $b = 1$ and $f(x) =\sqrt{x}$ so,

$$\int_0^1 \sqrt{x}\ dx = \dfrac2 3$$ should be the answer.

Is there any simpler method to do this sum ? I have not learnt this method to do infinite sums so I can't use it.

Answer 1

By the Stolz-Cesaro Theorem, one has \begin{eqnarray} &&\lim_{n \to \infty} \dfrac{\sqrt 1 + \sqrt 2 + \dots + \sqrt{n}}{n\sqrt{n}}\\ &=&\lim_{n \to \infty} \dfrac{\sqrt{n+1}}{(n+1)\sqrt{n+1}-n\sqrt n}\\ &=&\lim_{n \to \infty} \dfrac{\sqrt{n+1}}{(n+1)\sqrt{n+1}-n\sqrt n} \dfrac{(n+1)\sqrt{n+1}+n\sqrt n}{(n+1)\sqrt{n+1}+n\sqrt n}\\ &=&\lim_{n \to \infty} \dfrac{\sqrt{n+1}[(n+1)\sqrt{n+1}+n\sqrt n]}{(n+1)^3-n^3}\\ &=&\frac23. \end{eqnarray}

Answer 2

picture......................................

$$ \frac{2}{3} n \sqrt n < \mbox{SUM} < \frac{2}{3} \left( \; (n+1) \sqrt {n+1} \; - \; 1 \right) \; < \; \frac{2}{3} \left( \; (n+1) ( 1 +\sqrt n) \; - \; 1 \right) = \frac{2}{3} \left( \; n \sqrt n + n + \sqrt n \right) $$ $$ \frac{2}{3} n \sqrt n < \mbox{SUM} < \frac{2}{3} \left( \; n \sqrt n + n + \sqrt n \right) $$

For anyone worried about the little estimate above, $$ n + 1 < n + 2 \sqrt n + 1, $$ $$ \sqrt {n+1} \; \; < \; \; 1 + \sqrt n. $$

Answer 3

Learning new techniques is good:

Method to express the infinite series as definite integral:

$1.$ Express the given series in the form $\sum\frac{1}{n}f(\frac{r}{n})$.

$2.$ Then the limit is its sum when $n\to \infty$, i.e, $\lim_{n\to\infty}\sum\frac{1}{n}f(\frac{r}{n})$

$3.$ Replace $\frac{r}{n}$ by $x$ and $\frac{1}{n}$ by $dx$ and $\lim_{n\to\infty}\sum$ by $\int$

$4.$ The upper and lower limit are limiting values of $\frac{r}{n}$ for first and last term of $r$ respectively.

For instance: $\sum_{r=1}^n=\int\frac{1}{n}f(\frac{r}{n})=\int_0^1f(x).dx$.

Now, let's see your question:

$\lim_{n \to \infty} \dfrac{\sqrt 1 + \sqrt 2 + \dots + \sqrt{n}}{n\sqrt{n}}=\lim_{n \to \infty} \dfrac{1}{n}\sum_{r=1}^n\sqrt{\frac{r}{n}}=\int_0^1\sqrt{x}=\frac{2}{3}$.