1

Is there a method that works most of the times to simplify or decompose a quadratic form in order to simply read off the signature ?

I have this example:

$q(x, y, z, t, s) = xy − xt + yz − yt + ys + zt − zs + 2st$

What is the method or what prinicple should I keep in mind in order to get it correctly and as shortly as possible?

What I mean by "reading off" is putting it into this form:

$q(x, y, z, t, s) = 1/4(x +y+z+s-2t)^2 + 1/4(x+z+s)^2 - (t-z-3/2s)^2 + (z+s)^2 + 5/4s^2 $

Leroy
  • 511
  • If your form is defined over a field; you can diagonalized it; then you can compute the signnature easilly. – Davood Aug 28 '17 at 21:27
  • 1
    We can find a matrix $P$ with rational entries and $\det P = \pm 1$ so that $P^T H P = D$ is diagonal, where $H$ is the Hessian matrix of second partial derivatives of your form. See http://math.stackexchange.com/questions/1388421/reference-for-linear-algebra-books-that-teach-reverse-hermite-method-for-symmetr – Will Jagy Aug 28 '17 at 21:28
  • I got that, the question is, how do I get there just by simplifying the expression? – Leroy Aug 28 '17 at 21:48
  • It now appears that the expression you typed in is incorrect. See the method at the question I linked, and the further links there. Also check your expression. – Will Jagy Aug 28 '17 at 21:51
  • 1
    @Famke see my answer. My impression is that this is taught in many countries in a first linear algebra course, but not usually in the U.S. I was surprised when I came across this method. – Will Jagy Aug 28 '17 at 22:35
  • @Will Jagy ; My dear Will, this method surprised me too. – Davood Aug 29 '17 at 05:32

1 Answers1

2

October:

$$ P^T H P = D $$ $$ Q^T D Q = H $$ $$ H = \left( \begin{array}{rrrrr} 0 & 1 & 0 & - 1 & 0 \\ 1 & 0 & 1 & - 1 & 1 \\ 0 & 1 & 0 & 0 & - 1 \\ - 1 & - 1 & 0 & 0 & 2 \\ 0 & 1 & - 1 & 2 & 0 \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0 \\ - 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrrr} 2 & 1 & 1 & - 2 & 1 \\ 1 & 0 & 1 & - 1 & 1 \\ 1 & 1 & 0 & 0 & - 1 \\ - 2 & - 1 & 0 & 0 & 2 \\ 1 & 1 & - 1 & 2 & 0 \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrrr} 1 & - \frac{ 1 }{ 2 } & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrrr} 1 & - \frac{ 1 }{ 2 } & 0 & 0 & 0 \\ 1 & \frac{ 1 }{ 2 } & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrrr} \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & 0 & 0 & 0 \\ - 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrrr} 2 & 0 & 1 & - 2 & 1 \\ 0 & - \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & 0 & \frac{ 1 }{ 2 } \\ 1 & \frac{ 1 }{ 2 } & 0 & 0 & - 1 \\ - 2 & 0 & 0 & 0 & 2 \\ 1 & \frac{ 1 }{ 2 } & - 1 & 2 & 0 \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrrr} 1 & 0 & - \frac{ 1 }{ 2 } & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrrr} 1 & - \frac{ 1 }{ 2 } & - \frac{ 1 }{ 2 } & 0 & 0 \\ 1 & \frac{ 1 }{ 2 } & - \frac{ 1 }{ 2 } & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrrr} \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & 0 & 0 \\ - 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrrr} 2 & 0 & 0 & - 2 & 1 \\ 0 & - \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & 0 & \frac{ 1 }{ 2 } \\ 0 & \frac{ 1 }{ 2 } & - \frac{ 1 }{ 2 } & 1 & - \frac{ 3 }{ 2 } \\ - 2 & 0 & 1 & 0 & 2 \\ 1 & \frac{ 1 }{ 2 } & - \frac{ 3 }{ 2 } & 2 & 0 \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrrr} 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrrr} 1 & - \frac{ 1 }{ 2 } & - \frac{ 1 }{ 2 } & 1 & 0 \\ 1 & \frac{ 1 }{ 2 } & - \frac{ 1 }{ 2 } & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrrr} \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & - 1 & 0 \\ - 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrrr} 2 & 0 & 0 & 0 & 1 \\ 0 & - \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & 0 & \frac{ 1 }{ 2 } \\ 0 & \frac{ 1 }{ 2 } & - \frac{ 1 }{ 2 } & 1 & - \frac{ 3 }{ 2 } \\ 0 & 0 & 1 & - 2 & 3 \\ 1 & \frac{ 1 }{ 2 } & - \frac{ 3 }{ 2 } & 3 & 0 \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrrr} 1 & 0 & 0 & 0 & - \frac{ 1 }{ 2 } \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrrr} 1 & - \frac{ 1 }{ 2 } & - \frac{ 1 }{ 2 } & 1 & - \frac{ 1 }{ 2 } \\ 1 & \frac{ 1 }{ 2 } & - \frac{ 1 }{ 2 } & 1 & - \frac{ 1 }{ 2 } \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrrr} \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & - 1 & \frac{ 1 }{ 2 } \\ - 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrrr} 2 & 0 & 0 & 0 & 0 \\ 0 & - \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & 0 & \frac{ 1 }{ 2 } \\ 0 & \frac{ 1 }{ 2 } & - \frac{ 1 }{ 2 } & 1 & - \frac{ 3 }{ 2 } \\ 0 & 0 & 1 & - 2 & 3 \\ 0 & \frac{ 1 }{ 2 } & - \frac{ 3 }{ 2 } & 3 & - \frac{ 1 }{ 2 } \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrrr} 1 & - \frac{ 1 }{ 2 } & - 1 & 1 & - \frac{ 1 }{ 2 } \\ 1 & \frac{ 1 }{ 2 } & 0 & 1 & - \frac{ 1 }{ 2 } \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrrr} \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & - 1 & \frac{ 1 }{ 2 } \\ - 1 & 1 & - 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrrr} 2 & 0 & 0 & 0 & 0 \\ 0 & - \frac{ 1 }{ 2 } & 0 & 0 & \frac{ 1 }{ 2 } \\ 0 & 0 & 0 & 1 & - 1 \\ 0 & 0 & 1 & - 2 & 3 \\ 0 & \frac{ 1 }{ 2 } & - 1 & 3 & - \frac{ 1 }{ 2 } \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrrr} 1 & - \frac{ 1 }{ 2 } & - 1 & 1 & - 1 \\ 1 & \frac{ 1 }{ 2 } & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrrr} \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & - 1 & \frac{ 1 }{ 2 } \\ - 1 & 1 & - 1 & 0 & - 1 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrrr} 2 & 0 & 0 & 0 & 0 \\ 0 & - \frac{ 1 }{ 2 } & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & - 1 \\ 0 & 0 & 1 & - 2 & 3 \\ 0 & 0 & - 1 & 3 & 0 \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrrr} 1 & - \frac{ 1 }{ 2 } & 1 & - 1 & - 1 \\ 1 & \frac{ 1 }{ 2 } & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrrr} \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & - 1 & \frac{ 1 }{ 2 } \\ - 1 & 1 & - 1 & 0 & - 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrrr} 2 & 0 & 0 & 0 & 0 \\ 0 & - \frac{ 1 }{ 2 } & 0 & 0 & 0 \\ 0 & 0 & - 2 & 1 & 3 \\ 0 & 0 & 1 & 0 & - 1 \\ 0 & 0 & 3 & - 1 & 0 \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & \frac{ 1 }{ 2 } & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrrr} 1 & - \frac{ 1 }{ 2 } & 1 & - \frac{ 1 }{ 2 } & - 1 \\ 1 & \frac{ 1 }{ 2 } & 1 & \frac{ 1 }{ 2 } & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & \frac{ 1 }{ 2 } & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrrr} \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & - 1 & \frac{ 1 }{ 2 } \\ - 1 & 1 & - 1 & 0 & - 1 \\ 0 & 0 & - \frac{ 1 }{ 2 } & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrrr} 2 & 0 & 0 & 0 & 0 \\ 0 & - \frac{ 1 }{ 2 } & 0 & 0 & 0 \\ 0 & 0 & - 2 & 0 & 3 \\ 0 & 0 & 0 & \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } \\ 0 & 0 & 3 & \frac{ 1 }{ 2 } & 0 \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & \frac{ 3 }{ 2 } \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrrr} 1 & - \frac{ 1 }{ 2 } & 1 & - \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } \\ 1 & \frac{ 1 }{ 2 } & 1 & \frac{ 1 }{ 2 } & \frac{ 3 }{ 2 } \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & \frac{ 1 }{ 2 } & \frac{ 3 }{ 2 } \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrrr} \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & - 1 & \frac{ 1 }{ 2 } \\ - 1 & 1 & - 1 & 0 & - 1 \\ 0 & 0 & - \frac{ 1 }{ 2 } & 1 & - \frac{ 3 }{ 2 } \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrrr} 2 & 0 & 0 & 0 & 0 \\ 0 & - \frac{ 1 }{ 2 } & 0 & 0 & 0 \\ 0 & 0 & - 2 & 0 & 0 \\ 0 & 0 & 0 & \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } \\ 0 & 0 & 0 & \frac{ 1 }{ 2 } & \frac{ 9 }{ 2 } \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & - 1 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrrr} 1 & - \frac{ 1 }{ 2 } & 1 & - \frac{ 1 }{ 2 } & 1 \\ 1 & \frac{ 1 }{ 2 } & 1 & \frac{ 1 }{ 2 } & 1 \\ 0 & 0 & 0 & 1 & - 1 \\ 0 & 0 & 1 & \frac{ 1 }{ 2 } & 1 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrrr} \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & - 1 & \frac{ 1 }{ 2 } \\ - 1 & 1 & - 1 & 0 & - 1 \\ 0 & 0 & - \frac{ 1 }{ 2 } & 1 & - \frac{ 3 }{ 2 } \\ 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrrr} 2 & 0 & 0 & 0 & 0 \\ 0 & - \frac{ 1 }{ 2 } & 0 & 0 & 0 \\ 0 & 0 & - 2 & 0 & 0 \\ 0 & 0 & 0 & \frac{ 1 }{ 2 } & 0 \\ 0 & 0 & 0 & 0 & 4 \\ \end{array} \right) $$

==============================================

$$ P^T H P = D $$ $$\left( \begin{array}{rrrrr} 1 & 1 & 0 & 0 & 0 \\ - \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & 0 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 \\ - \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & 1 & \frac{ 1 }{ 2 } & 0 \\ 1 & 1 & - 1 & 1 & 1 \\ \end{array} \right) \left( \begin{array}{rrrrr} 0 & 1 & 0 & - 1 & 0 \\ 1 & 0 & 1 & - 1 & 1 \\ 0 & 1 & 0 & 0 & - 1 \\ - 1 & - 1 & 0 & 0 & 2 \\ 0 & 1 & - 1 & 2 & 0 \\ \end{array} \right) \left( \begin{array}{rrrrr} 1 & - \frac{ 1 }{ 2 } & 1 & - \frac{ 1 }{ 2 } & 1 \\ 1 & \frac{ 1 }{ 2 } & 1 & \frac{ 1 }{ 2 } & 1 \\ 0 & 0 & 0 & 1 & - 1 \\ 0 & 0 & 1 & \frac{ 1 }{ 2 } & 1 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) = \left( \begin{array}{rrrrr} 2 & 0 & 0 & 0 & 0 \\ 0 & - \frac{ 1 }{ 2 } & 0 & 0 & 0 \\ 0 & 0 & - 2 & 0 & 0 \\ 0 & 0 & 0 & \frac{ 1 }{ 2 } & 0 \\ 0 & 0 & 0 & 0 & 4 \\ \end{array} \right) $$ $$ Q^T D Q = H $$ $$\left( \begin{array}{rrrrr} \frac{ 1 }{ 2 } & - 1 & 0 & 0 & 0 \\ \frac{ 1 }{ 2 } & 1 & 0 & 0 & 0 \\ \frac{ 1 }{ 2 } & - 1 & - \frac{ 1 }{ 2 } & 1 & 0 \\ - 1 & 0 & 1 & 0 & 0 \\ \frac{ 1 }{ 2 } & - 1 & - \frac{ 3 }{ 2 } & 1 & 1 \\ \end{array} \right) \left( \begin{array}{rrrrr} 2 & 0 & 0 & 0 & 0 \\ 0 & - \frac{ 1 }{ 2 } & 0 & 0 & 0 \\ 0 & 0 & - 2 & 0 & 0 \\ 0 & 0 & 0 & \frac{ 1 }{ 2 } & 0 \\ 0 & 0 & 0 & 0 & 4 \\ \end{array} \right) \left( \begin{array}{rrrrr} \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & - 1 & \frac{ 1 }{ 2 } \\ - 1 & 1 & - 1 & 0 & - 1 \\ 0 & 0 & - \frac{ 1 }{ 2 } & 1 & - \frac{ 3 }{ 2 } \\ 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) = \left( \begin{array}{rrrrr} 0 & 1 & 0 & - 1 & 0 \\ 1 & 0 & 1 & - 1 & 1 \\ 0 & 1 & 0 & 0 & - 1 \\ - 1 & - 1 & 0 & 0 & 2 \\ 0 & 1 & - 1 & 2 & 0 \\ \end{array} \right) $$

I have found a correct expression $Q^T D Q = H,$ where $H$ is the Hessian matrix of your quadratic form. Let me first paste in $D,Q,H.$ Note that $D$ has three positive (diagonal) entries and two negative, which is correct. Your expression is wrong.

Moving some denominators around to save typing, I get

$$ \frac{1}{4} \left( x + y + z - 2t +s \right)^2 -\frac{1}{4} \left( -x + y - z -s \right)^2 -\frac{1}{4} \left( - z + 2t -3s \right)^2 + \frac{1}{4} \left( z +s \right)^2 + 2 s^2 $$ which is just one of infinitely many correct expressions possible. Now that I see how nicely this comes out, I would say this is an error-reduction idea: for each row in $Q$ where some coefficients are not integers, find the least common multiple of all the denominators, call that $n.$ Then multiply that row of $Q$ by $n$ but divide that entry in $D$ by $n^2.$ The outcome is that $D$ now has more fractions, but $Q$ is now all integers. 

? 
? form
%45 = (y - t)*x + ((z + (-t + s))*y + (-s*z + 2*s*t))
? 
?  me =  (1/4) * ( x + y + z - 2*t +s )^2 -(1/4) * ( -x + y - z  -s )^2 - (1/4) * (  - z + 2*t  -3*s )^2  + (1/4) * (   z +s )^2  + 2 * s^2

%46 = (y - t)*x + ((z + (-t + s))*y + (-s*z + 2*s*t))
? 
? me - form
%47 = 0
?

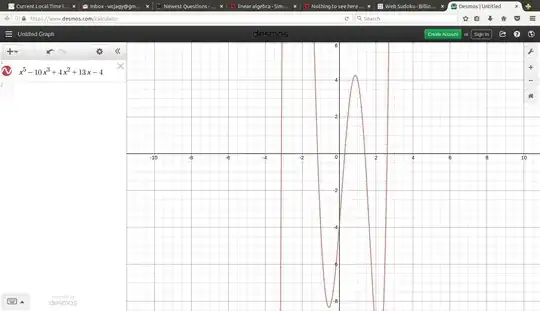
I guess I will put it here, this is a graph of the characteristic polynomial of the matrix $H,$ irreducible, five irrational real roots, three positive, two negative.

? p = charpoly(h)
%2 = x^5 - 10*x^3 + 4*x^2 + 13*x - 4
? factor(p)
%3 = 
[x^5 - 10*x^3 + 4*x^2 + 13*x - 4 1]

enter image description here

The algorithm I used is at reference for linear algebra books that teach reverse Hermite method for symmetric matrices

==============================================================

? d
%29 = 
[2 0 0 0 0]

[0 -1/2 0 0 0]

[0 0 -2 0 0]

[0 0 0 1/2 0]

[0 0 0 0 4]

? q
%30 = 
[1/2 1/2 1/2 -1 1/2]

[-1 1 -1 0 -1]

[0 0 -1/2 1 -3/2]

[0 0 1 0 1]

[0 0 0 0 1]

? h
%31 = 
[0 1 0 -1 0]

[1 0 1 -1 1]

[0 1 0 0 -1]

[-1 -1 0 0 2]

[0 1 -1 2 0]

?

==================================================

Here is how I found them:

parisize = 4000000, primelimit = 500509
?  h = [ 0,1,0,-1,0; 1,0,1,-1,1; 0,1,0,0,-1; -1,-1,0,0,2; 0,1,-1,2,0] 
%1 = 
[0 1 0 -1 0]

[1 0 1 -1 1]

[0 1 0 0 -1]

[-1 -1 0 0 2]

[0 1 -1 2 0]

? id = [ 1,0,0,0,0; 0,1,0,0,0; 0,0,1,0,0; 0,0,0,1,0; 0,0,0,0,1]
%2 = 
[1 0 0 0 0]

[0 1 0 0 0]

[0 0 1 0 0]

[0 0 0 1 0]

[0 0 0 0 1]

? p1 = [ 1,0,0,0,0; 1,1,0,0,0; 0,0,1,0,0; 0,0,0,1,0; 0,0,0,0,1]
%3 = 
[1 0 0 0 0]

[1 1 0 0 0]

[0 0 1 0 0]

[0 0 0 1 0]

[0 0 0 0 1]

? p1t = mattranspose(p1)
%4 = 
[1 1 0 0 0]

[0 1 0 0 0]

[0 0 1 0 0]

[0 0 0 1 0]

[0 0 0 0 1]

? d1 = p1t * h * p1
%5 = 
[2 1 1 -2 1]

[1 0 1 -1 1]

[1 1 0 0 -1]

[-2 -1 0 0 2]

[1 1 -1 2 0]

? p2 = [ 1,-1/2,-1/2,1,-1/2; 0,1,0,0,0; 0,0,1,0,0; 0,0,0,1,0; 0,0,0,0,1]
%6 = 
[1 -1/2 -1/2 1 -1/2]

[0 1 0 0 0]

[0 0 1 0 0]

[0 0 0 1 0]

[0 0 0 0 1]

? p2t = mattranspose(p2)
%7 = 
[1 0 0 0 0]

[-1/2 1 0 0 0]

[-1/2 0 1 0 0]

[1 0 0 1 0]

[-1/2 0 0 0 1]

? d2 = p2t * d1 * p2
%8 = 
[2 0 0 0 0]

[0 -1/2 1/2 0 1/2]

[0 1/2 -1/2 1 -3/2]

[0 0 1 -2 3]

[0 1/2 -3/2 3 -1/2]

? p3 = [ 1,0,0,0,0; 0,1,1,0,1; 0,0,1,0,0; 0,0,0,1,0; 0,0,0,0,1]
%9 = 
[1 0 0 0 0]

[0 1 1 0 1]

[0 0 1 0 0]

[0 0 0 1 0]

[0 0 0 0 1]

? p3t = mattranspose(p3)
%10 = 
[1 0 0 0 0]

[0 1 0 0 0]

[0 1 1 0 0]

[0 0 0 1 0]

[0 1 0 0 1]

? d3 = p3t * d2 * p3
%11 = 
[2 0 0 0 0]

[0 -1/2 0 0 0]

[0 0 0 1 -1]

[0 0 1 -2 3]

[0 0 -1 3 0]

? p4 = [ 1,0,0,0,0; 0,1,0,0,0; 0,0,0,1,0; 0,0,1,0,0; 0,0,0,0,1]
%12 = 
[1 0 0 0 0]

[0 1 0 0 0]

[0 0 0 1 0]

[0 0 1 0 0]

[0 0 0 0 1]

? p4t = mattranspose(p4)
%13 = 
[1 0 0 0 0]

[0 1 0 0 0]

[0 0 0 1 0]

[0 0 1 0 0]

[0 0 0 0 1]

? d4 = p4t * d3 * p4
%14 = 
[2 0 0 0 0]

[0 -1/2 0 0 0]

[0 0 -2 1 3]

[0 0 1 0 -1]

[0 0 3 -1 0]

? p5 = [ 1,0,0,0,0; 0,1,0,0,0; 0,0,1,1/2,3/2; 0,0,0,1,0; 0,0,0,0,1]
%15 = 
[1 0 0 0 0]

[0 1 0 0 0]

[0 0 1 1/2 3/2]

[0 0 0 1 0]

[0 0 0 0 1]

? p5t = mattranspose(p5)
%16 = 
[1 0 0 0 0]

[0 1 0 0 0]

[0 0 1 0 0]

[0 0 1/2 1 0]

[0 0 3/2 0 1]

? d5 = p5t * d4 * p5
%17 = 
[2 0 0 0 0]

[0 -1/2 0 0 0]

[0 0 -2 0 0]

[0 0 0 1/2 1/2]

[0 0 0 1/2 9/2]

? p6 = [ 1,0,0,0,0; 0,1,0,0,0; 0,0,1,0,0; 0,0,0,1,-1; 0,0,0,0,1]
%18 = 
[1 0 0 0 0]

[0 1 0 0 0]

[0 0 1 0 0]

[0 0 0 1 -1]

[0 0 0 0 1]

? p6t = mattranspose(p6)
%19 = 
[1 0 0 0 0]

[0 1 0 0 0]

[0 0 1 0 0]

[0 0 0 1 0]

[0 0 0 -1 1]

? d6 = p6t * d5 * p6
%20 = 
[2 0 0 0 0]

[0 -1/2 0 0 0]

[0 0 -2 0 0]

[0 0 0 1/2 0]

[0 0 0 0 4]

? p = p1 * p2 * p3 * p4 * p5 * p6
%21 = 
[1 -1/2 1 -1/2 1]

[1 1/2 1 1/2 1]

[0 0 0 1 -1]

[0 0 1 1/2 1]

[0 0 0 0 1]

? matdet(p)
%22 = -1
? q = - matadjoint(p)
%23 = 
[1/2 1/2 1/2 -1 1/2]

[-1 1 -1 0 -1]

[0 0 -1/2 1 -3/2]

[0 0 1 0 1]

[0 0 0 0 1]

? d = d6
%24 = 
[2 0 0 0 0]

[0 -1/2 0 0 0]

[0 0 -2 0 0]

[0 0 0 1/2 0]

[0 0 0 0 4]

? qt = mattranspose(q)
%25 = 
[1/2 -1 0 0 0]

[1/2 1 0 0 0]

[1/2 -1 -1/2 1 0]

[-1 0 1 0 0]

[1/2 -1 -3/2 1 1]

? qt * d * q
%26 = 
[0 1 0 -1 0]

[1 0 1 -1 1]

[0 1 0 0 -1]

[-1 -1 0 0 2]

[0 1 -1 2 0]

? h
%27 = 
[0 1 0 -1 0]

[1 0 1 -1 1]

[0 1 0 0 -1]

[-1 -1 0 0 2]

[0 1 -1 2 0]

? qt * d * q - h
%28 = 
[0 0 0 0 0]

[0 0 0 0 0]

[0 0 0 0 0]

[0 0 0 0 0]

[0 0 0 0 0]

? 
? d
%29 = 
[2 0 0 0 0]

[0 -1/2 0 0 0]

[0 0 -2 0 0]

[0 0 0 1/2 0]

[0 0 0 0 4]

? q
%30 = 
[1/2 1/2 1/2 -1 1/2]

[-1 1 -1 0 -1]

[0 0 -1/2 1 -3/2]

[0 0 1 0 1]

[0 0 0 0 1]

? h
%31 = 
[0 1 0 -1 0]

[1 0 1 -1 1]

[0 1 0 0 -1]

[-1 -1 0 0 2]

[0 1 -1 2 0]

?

==============================================

Will Jagy
  • 139,541