Geometrical meaning of $\operatorname{d}x$, $\operatorname{d}y$ and $\operatorname{d}y\over\operatorname{d}x$?

Question

I am also confused about whether these are symbols or have some meaning of their own. PS- I know that $\operatorname{d}y\over\operatorname{d}x$ geometrically represents the slope. But, I've come across $\operatorname{d}x\over\operatorname{d}y$ to make problems easier. What does $\operatorname{d}x\over\operatorname{d}y$ mean?

Answer 1

You should be very careful, those are merely notations.

$\frac{d\,y(x)}{d\,x}$ is the derivative of a variable $y$ with respect to $x$. It represents how much $y$ varies for small variations of $x$. If you draw the curve of $y(x)$, the derivative will be the slope, as you said.

The opposite works as well, if one can define $x$ as a function of $y$ (which is the same as inverting the function $y(x)$ - we must consider a subset of the image where it is injective to do so), you can differentiate it too: $\frac{d\,x(y)}{d\,y}$

But be careful! It is just a notation, it is not the division of $dx$ and $dy$, it is a limit as you can see here.

$\boxed{\frac{d\,y(x)}{d\,x} = \lim\limits_{h\rightarrow0} \frac{y(x+h)-y(x)}{h}}$

Here is some discussion about the meaning of $dx$ alone, pay attention to the commentary at the end: "Since I first posted this paper, two different people have emailed me to tell me that Real Mathematicians don't do this. Playing with dx in the ways described in this paper is apparently one of those smarmy tricks that physicists use to give headaches to mathematicians. "

Answer 2

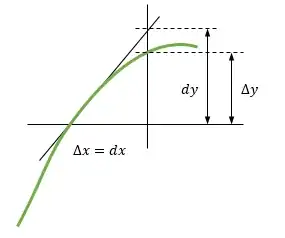
$dy$ represents the $y$ increment along the tangent. It is strictly proportional to $dx$.

$\Delta y$ represents the $y$ increment along the curve. It depends on the shape of the curve.

$\dfrac{dy}{dx}$ is the slope of the tangent, i.e. the derivative. $\dfrac{\Delta y}{\Delta x}$ approximates it for small $\Delta x$.

Answer 3

Here $\leftarrow$ is something I wrote about that.

$dx$ is thought of as an infinitely small but nonzero increment of $x$, just as $\Delta x$ is a finite increment of $x$.

$dy$ is the corresponding infinitely small increment of $y$.

Thus if at some point on the graph, $y$ is changing $3$ times as fast as $x$ is changing, then $dy=3\,dx$ at that point.

This is a quite useful heuristic even if not logically rigorous. Mathematicians have become extraordinarily squeamish about heuristics that are not logically rigorous, and that's why you don't often see this in textbooks today. Look at Silvanus Thompson's Calculus Made Easy.

Gottfried Wilhelm Leibniz introduced this notation in the 1600s.

Answer 4

Let's first start with $Δx$:

If you have two real numbers $x_0, x_1$, lets say $x_1>x_0$ you can calculate the different $x_1-x_0$. We define that difference as $Δx$: $$Δx:=x_1-x_0$$ With that difference we can also write: $$x_1 = x_0 + Δx.$$ or in words: If we add some change $Δx$ to $x_0$ we get $x_0+Δx$. That sounds trivial, but well it's just the definition of "change".

---

Well let us now look at functions. At first, let $f$ be a very simple function - a linear mapping: $$f:ℝ→ℝ \qquad x↦f(x)=mx + c.$$ Sometimes I will use $y=f(x)$, to simplify the notation. In that definition $m$ is the slope of the linear function, and $c$ the shift on the $y$-axis, since $f(0)=c$.

Since we learned how to write the change in $x$, we can try to write the change in $f(x)$, too. So we have: $$f(x+Δx) = m(x+Δx)+c = mx+mΔx+c.$$ Ok, that seems to be very boring.

But remember what we said above: Δx represents the change from $x_0$ to $x_0+Δx$. So if we now divide the change on the $y$-axis $Δy$ with the change on the $x$-axis we should get the something like the "rate of change" or the rate how "fast" $y$ changes relative to $x$. So let's do that: \begin{align*} \frac{Δy}{Δx}&=\frac{y_1-y_0}{Δx}=\frac{f(x_1) - f(x_0)}{Δx} = \frac{f(x_0+Δx) - f(x_0)}{Δx}\\ &=\frac{(mx+mΔx+c) - (mx+c)}{Δx}=\frac{mΔx}{Δx} = m. \end{align*} Pretty cool that we got the slope, as rate of change. Now we also see why that is the rate of change, if we divide by $Δx$: $$Δy = mΔx$$ So $m$ is the factor that tells you how large the change $Δ$ of $y$ is, if $x$ changes by $Δx$.

This quotient is called difference quotient or ratio of the differences.

---

Enough with these boring linear functions - we now look at arbitrary, but nice¹ functions: $$f:ℝ→ℝ,\qquad x↦f(x).$$

We can still look at the difference quotient - why the heck not? $$\frac{Δy}{Δx} = \frac{y_1-y_0}{(x_0+Δx) - x_0} = \frac{f(x_0+Δx) - f(x_0)}{(x_0+Δx) - x_0}$$ Uhm, well, now we are kind of stuck. But that is actually not that bad. Let's have a look at this picture from the German Wikipedia. Yes, I know it's German, but I think you will understand. Sekante = secant, Tangente = tanget, Funktionsgraph = graph, $x=x$ ...

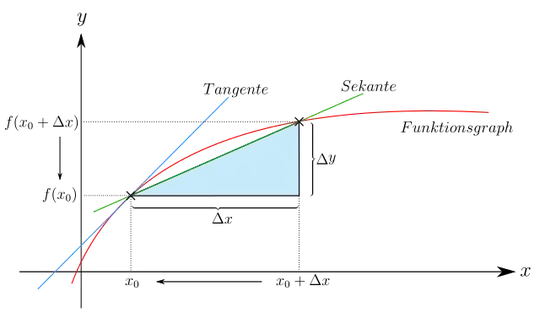
You can see the two crosses marking $(x_0,f(x_0))$ and $(x_0+Δx, f(x_0+Δx))$. So, our difference quotient represents the secant of the function $f$. Cool, but what does that mean?

Here is an example:
Today was really nice weather, and I made a trip by bike. Sometimes I was very slow, when there was a hill in my way. But on the other side I could ride very fast.
Since I own a smartphone, I was able to track the distance I travelled, and omniscient Google could also show me the graph of the distance I travelled as a function $f(x)$ at time $x$.

I started in the morning at $x_0=10:30$ and arrived at $x_1=17:00 = x_0+6.5\text{h}$ at my destination. Google says I travelled 130km. So I can calculate: $$\frac{Δy}{Δx} = \frac{130\text{km}}{6.5\text{h}} = 20 \frac{\text{km}}{\text{h}},$$ which is the average travelling velocity. And that is exactly what the slope of the secant represents. Just look at the picture above. (Well, I have to admit. If that red curve would represent the bike trip, it would be a very lame bike trip ...)

Now the average travelling speed is nice to know. But it would be very cool to know how fast my top speed was, don't you think? So now we are not interested in the average speed, but the speed in one point / current speed. Let's name it $f'(x_0)$.

Well, I don't know the definition of $f'$, yet. But if I calculate the average speed between two points $x_0$ and $x_1+Δx$ with a tiny, change $Δx$, doesn't that sound like a good approximation for "current speed"?

And since the average speed is the only thing that I know how to calculate, why not make $Δx$ smaller, and smaller, and smaller?
When we look at this process of making things "smaller and smaller" we call it a limit process, were we hope that at the end there is one value - the limit. If there is this limit, then it we use it to define "current speed": $$f'(x_0):= \lim_{Δx→0}\frac{Δy}{Δx} = \lim_{Δx→0}\frac{f(x_0+Δx)-f(x_0)}{Δx}$$

For a second let's take a step back, and look at the picture above. Imagine how the secant looks, if we make $Δx$ smaller and smaller. It will eventually hit the tangent. (Here you can look at an animation of that limit process, with a different function [$h=Δx$].)

So we learned that the secant represents the "average speed" and the tangent represents the "current speed". Pretty cool, don't you think?

---

Now what about this $\mathrm{d}x$?

Since mathematicians are usually very lazy² - I think everyone on this site will agree ;) - we like to invent new notations to write less.

So we write: $$f'(x_0)=\frac{\mathrm{d}f(x)}{\mathrm{d}x}\big|_{x=x_0} = \frac{\mathrm{d}f(x_0)}{\mathrm{d}x} =\frac{\mathrm{d}y}{\mathrm{d}x}.$$

In that notation we hide that actually there is this limit process above. These $\mathrm{dx}$'s or $\mathrm{dy}$'s are also called infinitesimals (=infinitely small increments). And the guy who invented this notation is Gottfried Leibniz (not to be confused with the cookie). The invention of this notation is a really cool thing, that helped a lot in modern calculus, after it was improved by Weierstraß.

---

Well almost done, but there is one part missing, that I did not answer so far:

But, I've come across dx/dy to make problems easier.

If you explain what you mean with that, I will gladly edit my answer. I just don't understand what you mean. Can you give an example of a problem that get's easier?

---

¹Nice meaning, that you don't have any jumps or "corners", as in $f(x)=|x|$, in the function values. ²Actually physicists are even lazier when it comes to writing ...

Answer 5

In the terms dx and dy, the d is for delta or "change in". So they represent the change in y and the change in x as a function, usually in terms of each other but sometimes another parameter. So dy/dx as you said is the slope, or change in x divided by the change in y, dy/dx is simply the inverse slope.

The different between dy and ∆y or dx and ∆x is that dy is a function that can be solved at any point to give the change in y at that point in relation to another variable, where as ∆y is a numerical value representing the difference in y between two points.