1

Let $$T[f(x),a]=\sum_{n=0}^\infty\frac{f^{(n)}(a)\,(x-a)^n}{n!}$$ given that $f:\mathbb{C}\to\mathbb{C}$, that $I\subseteq\mathbb{C}$, that $a\in I$, and that $f^{(n)}(a)$ exists for all $n\in\mathbb{N\cup\{0\}}$.

Does there exist some function $f$ such that $T[f(x),a]$ does not exist on $I$?

Remember that $\mathbb{R}\subset\mathbb{C}$, note that it is possible for $I$ to include or not include numbers that have imaginary parts, and note that functions $f:f(x)\neq T[f(x),a]$ are irrelevant if $T[f(x),a]$ is defined.

Edit 21 August 2017

After heavy consideration, I think this boils down to whether or not there exists a function such that $f^{(n)}(a)\ge n!$ as $n\to\infty$.

Edit 3 September 2017

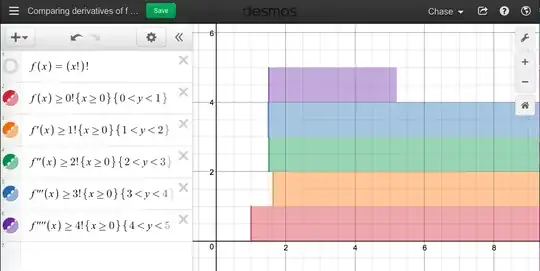
I have been considering the function $\Pi(x)=\Gamma(x+1)$. You can find a discussion about the very nasty $n$th derivative here. I did, however, run a graph of it through the web graphing calculator Desmos. Basically, each higher bar is a higher derivative of $\Pi(x)$, and it spans the positive interval on which $\Pi^{(n)}(x)\ge n!$

Desmos

Once I got to $\Pi^{(4)}(x)$, it started crashing, which is why the purple bar is incomplete (if it were meant to stop around $x=5.3$, then there would be a bold vertical line).

To me, this small sample seems to suggest that $\Pi^{(n)}(a)\ge n!$ for $a$ at least greater than or equal to $2$, which would make the coefficients of $T[\Pi(x),a]$ all be greater than or equal to $1$, so $T[\Pi(x),a]$ would diverge.

Martin Sleziak
  • 53,687
gen-ℤ ready to perish
  • 6,610
  • 5
    If a function has all derivatives at a point, its Taylor series exists. What may happen es that the series does not converge to the function. – Mariano Suárez-Álvarez Aug 20 '17 at 02:30
  • 1
    In $\mathbb{R}$, you want Borel's theorem. I don't understand completely the complex part of your question. Obviously you don't mean that $I$ can be an open set in $\mathbb{C}$ and that differentiability means that $f$ is holomorphic in $I$. If you only mean that $f$ is a $C^\infty$ function of 2 variables, then the Taylor series has a more complicated form. – Gribouillis Aug 20 '17 at 07:21
  • @Gribouillis Interesting. I mostly included $\mathbb{C}$ instead of $\mathbb{R}$ to learn something new. I'll have to read about this “more complicated form”! – gen-ℤ ready to perish Aug 21 '17 at 12:31

1 Answers1

1

Consider first $g: \mathbb R\to\mathbb R$, $$ g(x)=\left\{ \begin{array}{ccc} \mathrm{e}^{-1/x^2} & \text{if $x>0$},\\ 0 & \text{otherwise.} \end{array} \right. $$ Then $g\in C^\infty(\mathbb R)$, and $f^{(n)}(0)=0$, for all $n\in\mathbb N$. Thus the Taylor series $\sum_{n=0}^\infty \frac{g^{(n)}(0)\,x^n}{n!} $ exists but $g(x)\ne\sum_{n=0}^\infty \frac{g^{(n)}(0)\,x^n}{n!}$, for $x>0$.

Using this example, you can create similar situations for functions $f: \mathbb C\to\mathbb C$, when all partial derivatives in $x$ and $y$ exists.

Yiorgos S. Smyrlis
  • 83,933