2

A chain of four circles centered at A, B, C, and D are touched on one side by the line GH and on the other side by a circular arc EF centered at O. Find the area of D in terms of the areas of A, B, and C

The hint is to find the relationship between the radii of those circles and to convert them to their areas. Would it have anything to do with the formula for their common external tangents $x = 2\sqrt{r_1 r_2}$? Anyone have an idea? If it is not so much to ask, I would appreciate it too if someone could give a detailed answer. I'm quite slow at following with geometry. :(

http://sphotos-h.ak.fbcdn.net/hphotos-ak-prn1/32333_108091916020416_1986142595_n.jpg

Here is what I have so far:

(1) (2sqrt(rd) + d – c)^2 + (r-d-2 sqrt(cd))^2 = (r+c)^2

(2) (2sqrt(rd) + d – b)^2 + (r-d-2sqrt(cd) – 2sqrt(bc))^2 = (r+b)^2

(3) (2sqrt(rd) + d – a)^2 + (r-d-2sqrt(cd)-2sqrt(bc)-2sqrt(ab))^2 = (r+a)^2

Would this get somewhere?

John Chang
  • 758
  • Knowing the lengths $|OE|$ and $|EH|$, it's possible to find the radius of circle $D$ and thus its surface area using nothing more fancy than the Pythogerean theorem and from there on you can build up towards determining the other radii in the same fashion. – Raskolnikov Nov 11 '12 at 12:35
  • @Raskolnikov, Could you show me how sir? I'm not really good at geometry. :( – John Chang Nov 11 '12 at 13:17
  • @Raskolnikov, If We let OE = R and the radii of A,B,C,D be a,b,c,d respectively, we get that EH = 2sqrt(dR) + d.

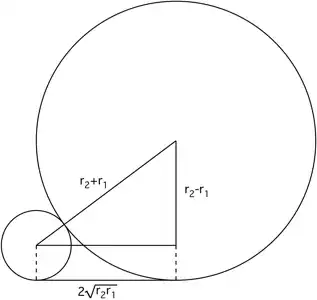
    How do we find the radius of D in terms of R? How do we work up to get the radii of the other circles? I can't seem to figure out how. And the problem states in terms of A,B,C. We have to eliminate the variable R as well. How could this be done sir?

     – John Chang Nov 11 '12 at 13:30
  • That's right, you know have an equation for $d$ which you can solve in terms of $R$ and $|EH|$. – Raskolnikov Nov 11 '12 at 13:36
  • @Raskolnikov What is the equation relating d and R? You mentioned using the pythagorean theorem. We get the OH is equal to sqrt( d^2 + r^2 + 4rd + 4dsqrt(dr)). Or am I getting the length of the wrong segment? I am sorry if I am slow at catching up sir. – John Chang Nov 11 '12 at 13:53

1 Answers1

4

Point 1: for two tangent circles, of radius $r_1$ and $r_2$, the distance between the points of tangency with a common external line is $2\sqrt{r_1r_2}$. This can be seen in this diagram:

$\hspace{4.5cm}$enter image description here

Point 2: The centers of the circles are all on a parabola with focus $O$ and directrix $\overline{GH}$.

Point 3: For a quadratic function $f$ and three values $x$, $y$, and $z$, $$ \frac{\dfrac{f(x)-f(y)}{x-y}-\dfrac{f(y)-f(z)}{y-z}}{x-z}\tag{1} $$ is constant.

Thus, we have $$ \frac{\dfrac{r_A-r_B}{\sqrt{r_Ar_B}}-\dfrac{r_B-r_C}{\sqrt{r_Br_C}}}{\sqrt{r_Ar_B}+\sqrt{r_Br_C}} =\frac{\dfrac{r_B-r_C}{\sqrt{r_Br_C}}-\dfrac{r_C-r_D}{\sqrt{r_Cr_D}}}{\sqrt{r_Br_C}+\sqrt{r_Cr_D}}\tag{2} $$ which can be solved as a quadratic in $\sqrt{r_D}$.

Simplification

The constant in $(1)$ is $\frac1{4f}$ where $f$ is the focal length of the parabola that passes through the centers of the circles. In fact, $(2)$ simplifies to $$ \frac1f=\frac1{r_B}-\frac1{\sqrt{r_Ar_C}}=\frac1{r_C}-\frac1{\sqrt{r_Br_D}}\tag{3} $$ Using $(3)$, it is easy to compute $f$ using $r_A$, $r_B$, and $r_C$, then it is easy to compute $r_D$ using $r_B$, $r_C$, and $f$.

Extension

With the bottoms of the circles on a horizontal line, circle $A$ on the left and $D$ on the right, the focus of the parabola is located at $$ x=\frac{r_A-r_B}{\sqrt{r_Ar_B}}f+\sqrt{r_Ar_B}\qquad\text{and}\qquad y=f-\frac{x^2}{4f}\tag{4} $$ relative to the center of circle $A$.

robjohn
  • 345,667