4

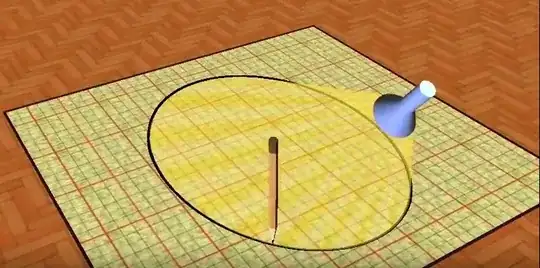
A light source with a right circular conical beam is placed at a height $h$ above the origin of the Cartesian $x$-$y$ plane (i.e. positioned at $(0,0,h)$), and directed vertically downwards. The resultant image on the Cartesian plane a circle with radius $b$ centred on the origin, i.e. $x^2+y^2=b^2$.

Now we want to move the light source along the positive $x$-axis, such that it is above $(k,0)$, but at height $z$ (i.e. positioned at $(k,0,z)$), and angle of incidence, $\alpha$, from the vertical such that the resultant image on the Cartesian plan is an ellipse centred on the origin with semi-minor axis $b$ and semi-major axis $a$ ($a>b$), i.e. $\frac {x^2}{a^2}+\frac{y^2}{b^2}=1$.

What are the values for the horizontal displacement $k$, height $z$ and angle of incidence $\alpha$ required to created the ellipse? (i.e. express $k$, $z$ and $\alpha$ in terms of $h, a, b$)

Here's a nice video on youtube by ElicaTeam illustrating something similar to the above. Here's a screenshot from the video.

enter image description here

Addendum

After further reflection, it may not be possible to find a solution under the given constraints. Whilst it may be possible to rotate the light source about $O$ such that the distance from $(0,\pm b)$ is always the same, the resultant ellipse will not be centred on $O$, and $(0,\pm b)$ will no longer be the vertices of the semi-minor axis of the ellipse.

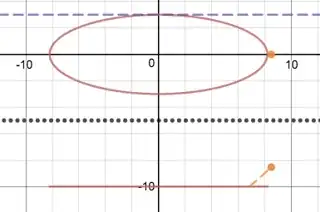
See simulation (plan view and side view) here.

For the required ellipse, perhaps a cone with a different aperture (or semi-vertical angle) is required.

Comments welcome.

enter image description here

Addendum II

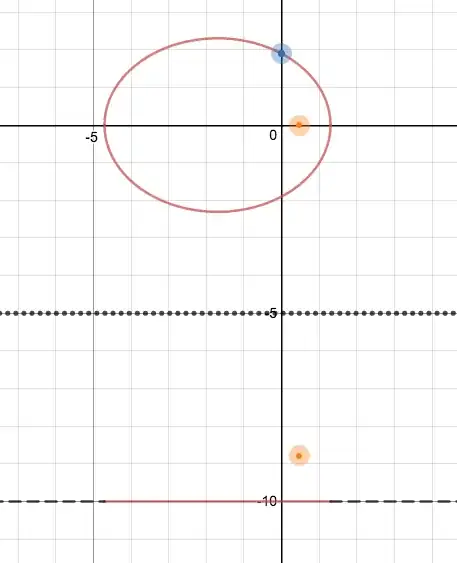
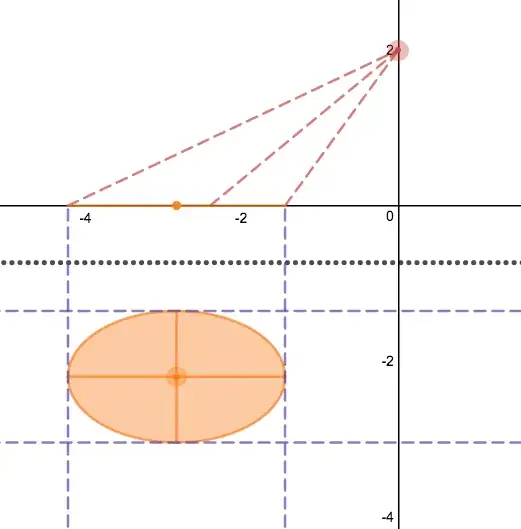
If we assume that the light cone aperture is fixed, then it is possible to create an ellipse-shaped "spotlight" centered on $O$, with semi-minor axis $b$ (specified) but with varying semi-major axis $a$, by changing the angle of tilt $\alpha$, the $x$-axis displacment $k$, and the $z$-axis displacement $z$.

See illustration here and screenshots below.

enter image description here

enter image description here

enter image description here

Addendum III (27 Jul 2017)*

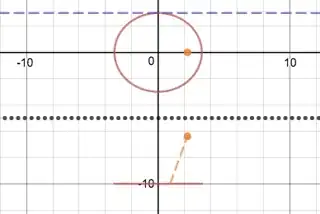
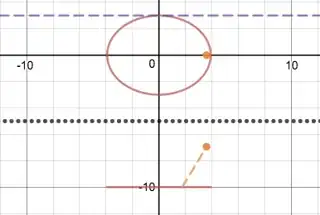
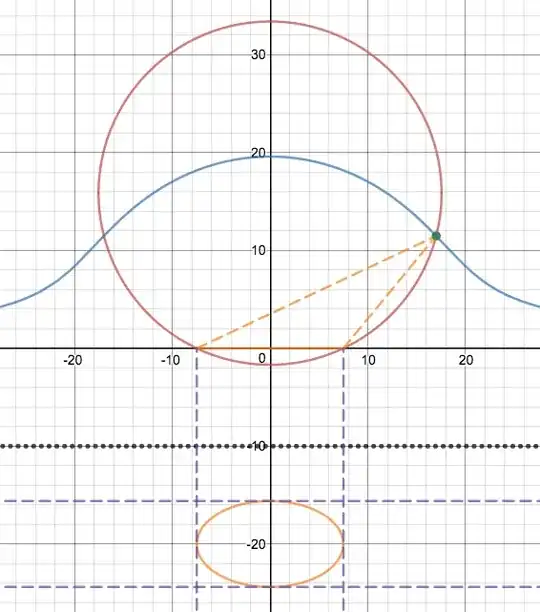
Per desmos implementation here it is NOT possible to obtain an origin-centred ellipse with semi-minor radius $b$, if the height of the light source remains the same. The blue curve is the locus of the light source for constant $b$. enter image description here

See also desmos implementation here which allows the resultant ellipse (not necessarily origin-centred) by varying light source position, beam angle and tilt angle.

enter image description here

Hypergeometricx
  • 22,657
  • Hint: as the semi minor axis is the same as the radius, the distance of the light source from the plane must be the same. – N74 Jul 05 '17 at 05:53
  • And the major axis is the minor axis divided by the cosine of the zenith angle ($\alpha$). – Cye Waldman Jul 05 '17 at 14:34
  • @N74 Logically so, but then $(0,b)$ may no longer necessarily be the vertex of the semi-minor axis. So the problem may not have a solution under the constraints provided. – Hypergeometricx Jul 06 '17 at 07:32
  • @CyeWaldman - This is the case for an inclined section of a cylinder but would it apply here for a cone? – Hypergeometricx Jul 06 '17 at 07:33
  • @hypergeometric On further refection, I think you may be correct. I'll have to look at again. Thanks for your observation. – Cye Waldman Jul 06 '17 at 13:31
  • I think this is possible, I made a construction in geogebra and I found a way to find the position of the ellipse. Too bad it would need a non linear system of equations to be solved. I will link a picture but I fear I shall not be able to explain how it works. – N74 Jul 07 '17 at 16:45
  • @N74 - If we assume that the light cone aperture is fixed, then it is possible to create an ellipse-shaped "spotlight" centered on $O$, with semi-minor axis $b$ (specified) but with varying semi-major axis $a$, by changing the angle of tilt $\alpha$, the $x$-axis displacment $k$, and the $z$-axis displacement $z$. – Hypergeometricx Jul 07 '17 at 17:26
  • Now the hard part is to find these parameters from $a$, $b$ and $h$. – N74 Jul 07 '17 at 19:21
  • @N74 - Yes, although technically that is a slightly different question (which I shall post separately); the answer to the question as posted above seems to be that there is no solution. – Hypergeometricx Jul 08 '17 at 17:16
  • It seems certain that a solution always exists. By changing $\alpha$ you can obtain any eccentricity (hence any ratio $a/b$) that you need, for a cone of any half vertex angle between zero and a right angle; by changing $z$ you can enlarge or shrink the ellipse until $a$ and $b$ have the desired values; by changing $k$ you can translate the center of the ellipse into the origin. The only difficulty is deriving the necessary values of $\alpha,$ $z,$ and $k.$ – David K Jul 08 '17 at 17:45
  • @DavidK - Yes but it won't be centred on the origin, as shown in the first diagram in the Addendum. – Hypergeometricx Jul 08 '17 at 17:48
  • 1
    If it is not centered on the origin, increase or decrease $k$ until it is. – David K Jul 08 '17 at 20:30
  • 2
    I think this question can be solved by setting $u=\arctan (b/h)$ and applying the solution of your follow-up question. – David K Jul 09 '17 at 00:22
  • This question seems relevant: https://math.stackexchange.com/questions/2226760/why-are-quadratic-equations-the-same-as-right-circular-conic-sections and links to an interesting note, https://arxiv.org/pdf/1708.07093.pdf – David K Jul 29 '18 at 00:11

1 Answers1

1

We know that every ellipse can be obtained by intersecting a right circular cone with a plane, in this case, the $x$-$y$ plane. The eccentricity $e$ of the ellipse determines the angle that the cone’s axis makes with this plane, while the size and position of the ellipse are determined by the location of the cone’s vertex.

Let the vertex of the cone be at $(v_x,0,v_z)$ and $0\le\theta\lt\frac\pi4$ be the angle that its axis makes with the $z$-axis. (For clarity, I’ve changed the variable names from those in the original problem statement. Using both $a$ and $\alpha$ in the same equations is just asking for trouble.) By rotating and translating the cone $x^2+y^2=z^2$, and then setting $z=0$, we can find after some manipulation that the intersection of the tilted and shifted cone with the $x$-$y$ plane is the conic given by the equation $$x^2\cos2\theta+y^2-2(v_x\cos2\theta-v_z\sin2\theta)x+(v_x^2-v_z^2)\cos2\theta-2v_xv_z\sin2\theta=0.\tag1$$ The center of this ellipse can be found by the usual technique of differentiation, which results in the condition $$v_x=v_z\tan2\theta\tag2$$ for its center to be at the origin. Substituting this back into (1) reduces the equation to $$x^2\cos2\theta+y^2=v_z^2\sec2\theta,\tag3$$ from which we get $$a^2=v_z^2\sec^22\theta\\b^2=v_z^2\sec2\theta$$ and finally $$v_z=\pm\frac{b^2}a, \cos2\theta={b^2\over a^2}=1-e^2.\tag4$$

To generalize this to a cone with arbitrary aperture angle $2\phi$, start with the equation $x^2+y^2=z^2\tan^2\phi$ instead, and proceed in a similar fashion.

amd
  • 53,693