5

After cutting a scotch egg into two to share, a friend and I wondered, "How many different ingredients can a solid mixture have, such that there exists a plane that splits the mixture into two halves, each having the same amount of each ingredient?"

I thought the answer was three. For example, a scotch egg has three ingredients: egg white, yolk and stuffing. Each ingredient has a centre of mass, and there is at least one plane that passes through any three arbitrary points.

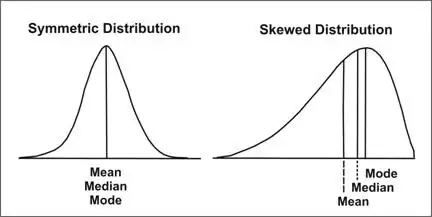
He later pointed out that the centre of mass does not necessarily divide a distribution into two. Looking at the one-dimensional case,

mean vs median

I should have used the median instead of the mean. Is there an equivalent "median of mass"?

Community
  • 1
Gnubie
  • 445
  • I should say that dividing along the proper principle axis will help in a symmetric cut. But also remember that COM is slightly different from mean as it's a mass weighted average, for a 2D shaped graph like the ones illustrated the COM and mean won't necessarily lie in the same spot – Triatticus Jul 04 '17 at 19:09
  • Exactly, that's why I thought I should have used the median instead of mean. But what is the equivalent of median for 3D shapes? – Gnubie Jul 04 '17 at 19:13
  • I'm actually not entirely sure – Triatticus Jul 04 '17 at 19:19
  • 1
    One equivalent of median for $3$-dimensional shapes is as follows. The center of gravity (assuming uniform density) of the region $R$ is the point $$ \operatorname{argmin}_c \iiint_R |(x,y,z) - c |^2 , d(x,y,z) $$ (and for non-uniform density, just multiply $d(x,y,z)$ by the density function). What is often called the "median" is $$ \operatorname{argmin}_c \iiint_R |(x,y,z) - c | , d(x,y,z). $$ This "median" is a lot more work to compute than the mean, which is the center of gravity. But I don't know whether this kind of median answers your question. $\qquad$ – Michael Hardy Jul 04 '17 at 19:51
  • Perhaps @Gnubie hasn't seen $\operatorname*{argmin}_c$ before. It means "the argument ($c$) that minimizes the expression". See https://en.wikipedia.org/wiki/Arg_max#Arg_min – md2perpe Jul 04 '17 at 20:44

1 Answers1

1

For your original question, the answer comes from the Ham Sandwich Theorem that for every positive integer $n$, given $n$ measurable objects in $n$-dimensional space, it is possible to divide all of them in half with a single $(n − 1)$-dimensional hyperplane.

So you are correct: in three dimensions, the three parts of your Scotch egg can each be divided into two parts of equal volumes by a single plane. This cannot be guaranteed for four parts (the breadcrumbs?).

I would call that plane a volume bisector. Similarly I would call a line which cut a two-dimensional area in half an area bisector, and in two dimensions you get the Pancake Theorem saying you can bisect two pancakes with a single line cut.

For a single triangle, the medians through a vertex and the midpoint of the opposite edge are area bisectors and the three medians intersect in the centroid of the triangle, but there are other area bisectors which do not pass through the centroid. I discussed this point in another question with this diagram, where the blue lines are medians and the green lines are other area bisectors

medians and area bisectors

Henry
  • 157,058