The general solution for Inviscid Burgers' Equation

Question

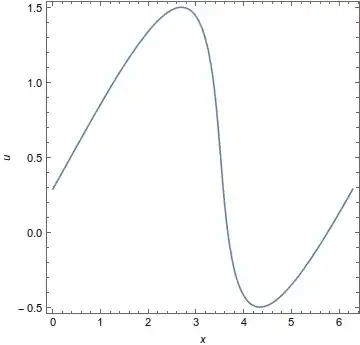
Hi I am trying to find the general solution of the following Inviscid Burgers' Equation

$$u_t+uu_x=0,\qquad u(x,0)=0.5+\sin x$$

So far I got the solution is $$u=0.5+\sin(x-ut)$$

Am I right? Also the solution is implicit. Now if I would like to draw the solution how would I do that?

Thanks in advance.

Your solution is correct. In general, solutions to burgers equation (and other quasi-linear pde) are implicit. — Jonathan Davidson, Jul 03 '17 at 07:43
To plot it, it might be easiest to plot the characteristic lines of constant u — KyleW, Jul 03 '17 at 08:54

score 3 · Accepted Answer · answered Jul 03 '17 at 18:50

There are a handful of scientific plotting programs that are able to plot implicit equations.

For instance, the following piece of code in Mathematica produces a plot of the solution in the $(x,u)$ plane for $t = 0.75$

ContourPlot[u == 1/2+Sin[x - u*0.75], {x, 0, 2*Pi}, {u, -0.5, 1.5}]

You can see what happens as you progress in time (in particular when you approach $t \to 1$) by introducing $t$ as some variable and embedding the snippet in a loop. Perhaps this is done more efficiently in Matlab though.

Hope this helps!

@mint Note that this method will provide a correct plot of the solution until the time where a shock occurs, i.e. the breaking time $t_B=\frac{−1}{\min ∂_x u(x,0)} = 1$. See e.g. this post. — EditPiAf, Dec 05 '17 at 18:49

The general solution for Inviscid Burgers' Equation

1 Answers1