The method of characteristics gives $u=f(x-ut)$ where $f(x) = \sin(x)$ represents the initial data $u(x,0)$. This implicit equation can be used to approach the solution, until a shock wave is met by the characteristics. Here is a sketch of the characteristics in the $x$-$t$ plane:
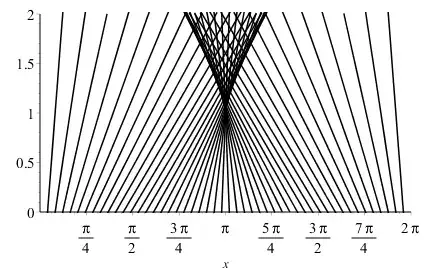
As shown in this post, the shock is formed when characteristics intersect for the first time, i.e. at the breaking position and time
\begin{aligned}
x_B &= \arg \min f'(x) = (2n+1)\pi
, \qquad (n\in \Bbb{Z})\\
t_B &= \frac{-1}{\min f'(x)} =1
\end{aligned}
as shown in the figure. Setting $v=-u$, one notes the relationship
$$
v(x_B - x, t) = \sin \left[x - v(x_B - x, t)\, t\right]
$$
which proves the symmetry property $u(x_B - x, t) = -u(x, t)$.
By solving the implicit equation $u = f(x-ut)$, the method of characteristics yields the values $u_L$, $u_R$ of $u$ on the left and the right of the shock. The position $(x_s(t), t)$ of the shock wave is given by the Rankine-Hugoniot condition
$$x'_s(t) = \tfrac{1}{2} (u_L+u_R)$$
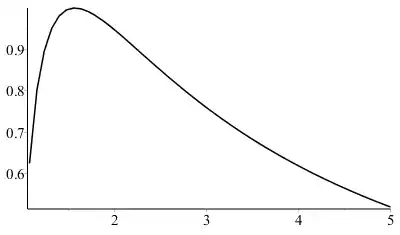
with initial position $x_s(t_B) = x_B$. Therefore, using symmetry $u_L = -u_R$, the shock wave remains at the same place (static shock). Its magnitude $u_L$ increases and then vanishes in time, as shown in the figure below, where $u_L$ --obtained numerically-- is plotted with respect to $t$: