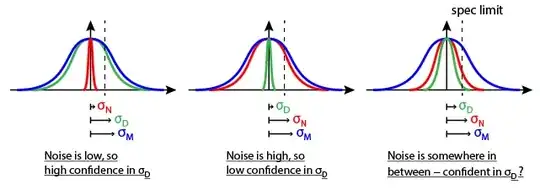
The question can be reduced to evaluation of the probability $\mathbb{P}(\hat{\sigma}_D < L)$, where $L>0$ is known. It is sufficient to calculate the CDF of $\hat{\sigma}_D$. Unfortunately, it appears no closed-form exists.
Part 1. We call secondary data the noise-only measures. They are a sequence $\{ y_1, \dots, y_n \}$ such that $y_i = n_i$, for $i=1,\dots,n$, where $n_i \sim \mathcal{N}(0, \sigma^2_N)$ are i.i.d. gaussian random variables (RVs), aka, noise. From standard estimation theory, (see note)
$$
\hat{\sigma}^2_N = \frac{1}{n} \sum_{i=1}^n y_i^2
$$
is the MLE (Maximum Likelihood Estimator) of $\sigma^2_N$ and it follows a $\chi^2$ distribution with $n$ degrees of freedom. More precisely:
$$
n \frac{\hat{\sigma}^2_N}{\sigma^2_N} \sim \chi^2_{n}
$$
Let $z_i$ denote primary data (signal+noise). We have that
$z_i = x_i + w_i$, for $i=1,\dots,n$, where: $x_i \sim \mathcal{N}(0, \sigma^2_D)$ represents the device, $w_i \sim \mathcal{N}(0, \sigma^2_N)$ is noise, independent of $x_i$ and $n_i$. Again,
$$
\hat{\sigma}^2_M = \frac{1}{n} \sum_{i=1}^n z_i^2
$$
from which
$$
n \frac{\hat{\sigma}^2_M}{\sigma^2_M} \sim \chi^2_n
$$
Note: There is no need to subtract the sample mean $\bar{y}$ since we know that $\mathbb{E}[y_i] = 0$. If you actually use
$$
\tilde{\sigma}^2_N = \frac{1}{n} \sum_{i=1}^n (y_i - \bar{y})^2
$$
this is not ML anymore. It still is $\chi^2$ distribution, but with $(n-1)$ degrees of freedom. More precisely, $(n-1)s^2 / \sigma^2 \sim \chi^2_{n-1}$, where $s^2$ is the unbiased sample variance, defined as: $s^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2$. The precise mathematical statement follows from Cochran's theorem.
Part 2. We know that $\rm Var[z_i] = Var[x_i] + Var[w_i]$, so we can compute
$$
\hat{\sigma}^2_D = \hat{\sigma}^2_M - \hat{\sigma}^2_N
$$
Essentially, we now need to compute the CDF of the difference between two independent $\chi^2$ RVs, which is not trivial. This is complicated by the fact that some coefficients are needed to make things right. We need to use the following result.
Lemma. Let $X,Y$ be two independent $\chi^2_n$. The PDF of $Z=X-Y$ is given by
$$
f_Z(z) = \frac{1}{\sqrt{\pi} 2^{n/2}} \frac{1}{\Gamma \Big( \frac{n}{2} \Big)} |z|^{(n-1)/2} K_{\frac{n-1}{2}}\Big( |z| \Big)
$$
where $K(\cdot)$ is the modified Bessel function of the second kind and $\Gamma(\cdot)$ is the Gamma function.
Proof. See here.
Denoting the PDF of $\hat{\sigma}^2_D$ with $f_Z(z)$, the CDF is given by
$$
\mathbb{P}(\hat{\sigma}^2_D \leq t) = F_Z(t) = \int_{-\infty}^t f_Z(z) dz
$$
Since $\hat{\sigma}_D = \sqrt{\hat{\sigma}^2_D}$, your solution is
$$
\mathbb{P}(\sqrt{\hat{\sigma}^2_D} < L) = \mathbb{P}(\hat{\sigma}^2_D < L^2) = F_Z(L^2) = \int_{-\infty}^{L^2} f_Z(z) dz
$$
which is the probability that the device is compliant.
ADDENDUM. To answer the accuracy question, define the Signal-to-Noise Ratio (SNR) as follows
$$
SNR = \frac{\sigma^2_D}{\sigma^2_N}
$$
which you can compute using estimated values (use big values of $n$, since, ideally, you would like to have $n \rightarrow +\infty$). SNR is a useful measure. First, $SNR \geq 0$ always. Second, in the limit $\sigma^2_N \rightarrow +\infty$ (infinitely powerful noise), we have $SNR=0$, while $\sigma^2_D \rightarrow +\infty$ (infinitely powerful signal) implies $SNR=+\infty$. In other words, the bigger the SNR, the better.
SNR is a quantitative metric tied to the accuracy of your measurements. Sometimes, you will see a threshold-based approach to define "accuracy": if $SNR \geq \gamma$, where $\gamma>0$ is arbitrarily decided (e.g. $\gamma = 10^3$), then you label the results as ``accurate'', inaccurate otherwise. But this approach is flawed, since accuracy is treated as a binary value, which is too simplistic.
A better approach is to compute
$$
\eta = 1 - \frac{1}{SNR +1}
$$
Why and how does this work? For $SNR=0$ (infinitely powerful noise or zero signal), $\eta=0$. For $SNR=+\infty$ (zero noise or infinitely powerful signal), $\eta=1$. So, clearly, $\eta \in [0,1]$, with extreme values taken only under limiting conditions. If you now use $a_{[\%]} = 100\eta$, you can interpret $a_{[\%]}$ directly as accuracy itself expressed in percentage. So, for example, $\eta=0.9$ implies 90% accurate measures, while $\eta=0.1$ implies rather inaccurate measures. This gives us a quantitative measure of the accuracy of our measures, which is also simple to calculate and intuitively appealing.