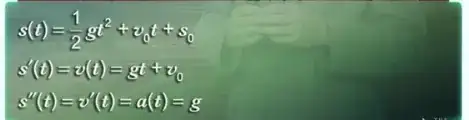In this example, the derivative of $x$ is $1(x^{1-1})$, and this is based on the application of the power rule.
But, what if $x$ is $0$? Can $x$ be differentiated? Zero to the power of zero is undefined.
And therefore when the subsequent example shown below:
$s'(t) = v(t) = gt + v_0$, where I assume the derivative of the sum of $2$ functions was applied.
I don't quite understand how the derivative of $\frac{d}{dx}[v_0t]$ was derived as $v_0$, based on the previous example of the power rule.
Can I see $\frac{d}{dx}[v_0t]$ as $v_0$ as a constant, multiplied by the function $f(t)$, and I shall apply the power rule as $v_0 \times d/dx[t]$, and it becomes $v_0 \times \frac{d}{dx}[t] = v_0 *\times 1 $?
$\frac{d}{dx}[\frac{1}{2}gt^2+v_0t+s_0] $ is
- $\frac{d}{dx}[\frac{1}{2} gt^2] = \frac{1}{2} \times 2 + gt^{(2-1) }= gt $
- $\frac{ d}{dx}[v_0t] = 1[v_0\times t^{(1-1)}]$
- $\frac{d}{dx}[s_0] = 0$, since the derivative of a constant is $0$