3

I am given the following symmetric matrix:

$$ A=\begin{pmatrix} 1 & 2 & 0 & 1\\ 2 & 0 & 3 & 0\\ 0 & 3 & -1 & 1\\ 1 & 0 & 1 & 4\\ \end{pmatrix}\in M_4(\Bbb R) $$ Let $f\in Bil(V), f(u,v)=u^tAv.$

I want to find a base $B \subset \Bbb R^4$ such that the matrix representing $f $ in respect to $B$ is diagonal.

I took $ v_1=\begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} $ and found a vector space $V_2=\{v\in\Bbb R^4$| $f(v,v_1)=0\}$, and got $V_2 =sp\{ \begin{pmatrix} -2 \\ 1 \\ 0 \\ 0 \end{pmatrix},\begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix},\begin{pmatrix} -1 \\ 0 \\ 0 \\ 1 \end{pmatrix}\} =sp\{v_2,v_3,v_4\}$

Now, the matrix in repect to $B=\{v_1,v_2,v_3,v_4\}$ looks like this:$$ \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & -4 & 3 & -2\\ 0 & 3 & -1 & 1\\ 0 & -2 & 1 & 3\\ \end{pmatrix} $$

I want to continue inductively, but I'm not sure how to procceed.

user401516
  • 2,383

4 Answers4

1

see http://math.stackexchange.com/questions/1388421/reference-for-linear-algebra-books-that-teach-reverse-hermite-method-for-symmetr

Also see jpegs at end of answer

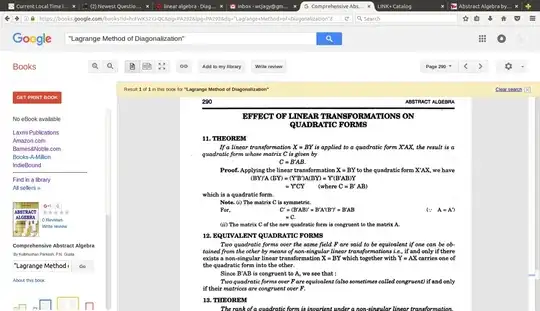
$$ P^T H P = D $$ $$ Q^T D Q = H $$ $$ H = \left( \begin{array}{rrrr} 1 & 2 & 0 & 1 \\ 2 & 0 & 3 & 0 \\ 0 & 3 & - 1 & 1 \\ 1 & 0 & 1 & 4 \\ \end{array} \right) $$

==============================================

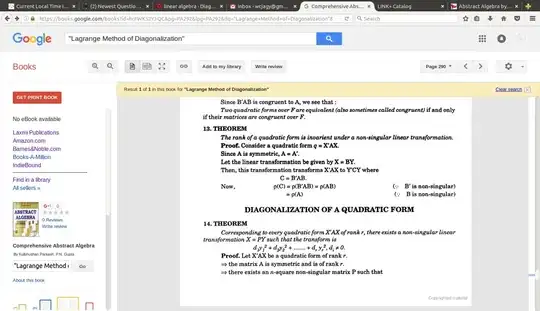
$$\left( \begin{array}{rrrr} 1 & - 2 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrr} 1 & - 2 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrr} 1 & 2 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrr} 1 & 0 & 0 & 1 \\ 0 & - 4 & 3 & - 2 \\ 0 & 3 & - 1 & 1 \\ 1 & - 2 & 1 & 4 \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrr} 1 & 0 & 0 & - 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrr} 1 & - 2 & 0 & - 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrr} 1 & 2 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & - 4 & 3 & - 2 \\ 0 & 3 & - 1 & 1 \\ 0 & - 2 & 1 & 3 \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & \frac{ 3 }{ 4 } & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrr} 1 & - 2 & - \frac{ 3 }{ 2 } & - 1 \\ 0 & 1 & \frac{ 3 }{ 4 } & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrr} 1 & 2 & 0 & 1 \\ 0 & 1 & - \frac{ 3 }{ 4 } & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & - 4 & 0 & - 2 \\ 0 & 0 & \frac{ 5 }{ 4 } & - \frac{ 1 }{ 2 } \\ 0 & - 2 & - \frac{ 1 }{ 2 } & 3 \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & - \frac{ 1 }{ 2 } \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrr} 1 & - 2 & - \frac{ 3 }{ 2 } & 0 \\ 0 & 1 & \frac{ 3 }{ 4 } & - \frac{ 1 }{ 2 } \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrr} 1 & 2 & 0 & 1 \\ 0 & 1 & - \frac{ 3 }{ 4 } & \frac{ 1 }{ 2 } \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & - 4 & 0 & 0 \\ 0 & 0 & \frac{ 5 }{ 4 } & - \frac{ 1 }{ 2 } \\ 0 & 0 & - \frac{ 1 }{ 2 } & 4 \\ \end{array} \right) $$

==============================================

$$\left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & \frac{ 2 }{ 5 } \\ 0 & 0 & 0 & 1 \\ \end{array} \right) $$ $$ P = \left( \begin{array}{rrrr} 1 & - 2 & - \frac{ 3 }{ 2 } & - \frac{ 3 }{ 5 } \\ 0 & 1 & \frac{ 3 }{ 4 } & - \frac{ 1 }{ 5 } \\ 0 & 0 & 1 & \frac{ 2 }{ 5 } \\ 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; Q = \left( \begin{array}{rrrr} 1 & 2 & 0 & 1 \\ 0 & 1 & - \frac{ 3 }{ 4 } & \frac{ 1 }{ 2 } \\ 0 & 0 & 1 & - \frac{ 2 }{ 5 } \\ 0 & 0 & 0 & 1 \\ \end{array} \right) , \; \; \; D = \left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & - 4 & 0 & 0 \\ 0 & 0 & \frac{ 5 }{ 4 } & 0 \\ 0 & 0 & 0 & \frac{ 19 }{ 5 } \\ \end{array} \right) $$

==============================================

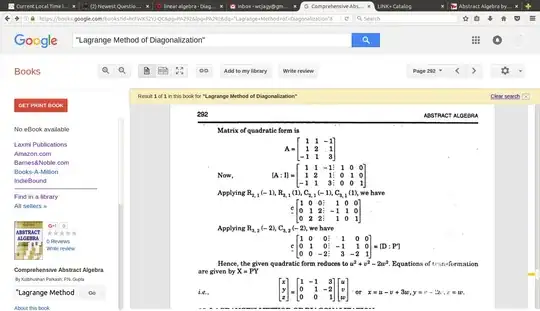
$$ P^T H P = D $$ $$\left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ - 2 & 1 & 0 & 0 \\ - \frac{ 3 }{ 2 } & \frac{ 3 }{ 4 } & 1 & 0 \\ - \frac{ 3 }{ 5 } & - \frac{ 1 }{ 5 } & \frac{ 2 }{ 5 } & 1 \\ \end{array} \right) \left( \begin{array}{rrrr} 1 & 2 & 0 & 1 \\ 2 & 0 & 3 & 0 \\ 0 & 3 & - 1 & 1 \\ 1 & 0 & 1 & 4 \\ \end{array} \right) \left( \begin{array}{rrrr} 1 & - 2 & - \frac{ 3 }{ 2 } & - \frac{ 3 }{ 5 } \\ 0 & 1 & \frac{ 3 }{ 4 } & - \frac{ 1 }{ 5 } \\ 0 & 0 & 1 & \frac{ 2 }{ 5 } \\ 0 & 0 & 0 & 1 \\ \end{array} \right) = \left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & - 4 & 0 & 0 \\ 0 & 0 & \frac{ 5 }{ 4 } & 0 \\ 0 & 0 & 0 & \frac{ 19 }{ 5 } \\ \end{array} \right) $$ $$ Q^T D Q = H $$ $$\left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 2 & 1 & 0 & 0 \\ 0 & - \frac{ 3 }{ 4 } & 1 & 0 \\ 1 & \frac{ 1 }{ 2 } & - \frac{ 2 }{ 5 } & 1 \\ \end{array} \right) \left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & - 4 & 0 & 0 \\ 0 & 0 & \frac{ 5 }{ 4 } & 0 \\ 0 & 0 & 0 & \frac{ 19 }{ 5 } \\ \end{array} \right) \left( \begin{array}{rrrr} 1 & 2 & 0 & 1 \\ 0 & 1 & - \frac{ 3 }{ 4 } & \frac{ 1 }{ 2 } \\ 0 & 0 & 1 & - \frac{ 2 }{ 5 } \\ 0 & 0 & 0 & 1 \\ \end{array} \right) = \left( \begin{array}{rrrr} 1 & 2 & 0 & 1 \\ 2 & 0 & 3 & 0 \\ 0 & 3 & - 1 & 1 \\ 1 & 0 & 1 & 4 \\ \end{array} \right) $$

=====================================================

enter image description here

enter image description here

enter image description here

Will Jagy
  • 139,541
0

It doesn't seem that it can be done in a straightforward way. The entries of the main diagonal of the matrix of $f$ with respect to the new basis are the roots of the characteristic polynomial of $A$, which is $x^4-4 x^3-16 x^2+61 x-19$. It seems to be irreducible in $\mathbb{Q}[x]$.

José Carlos Santos
  • 427,504
  • We don't change bases with matrices of bilinear forms as we do with matrices of linear transformations. In particular, the new matrix will be congruent but not necessarily similar. – Ben Grossmann Jun 23 '17 at 21:08
  • When we diagonalize the matrix of a bilinear form, the entries of the main diagonal pf the new matrix are the eigenvalues of the matrix $A$. Since, in this case, they are the roots of an irreducible quartic polynomial in $\mathbb{Q}[x]$, there can be no simple answer to the problem. – José Carlos Santos Jun 23 '17 at 21:18
  • Prof. Santos, especially on this site, the word Diagonalize is ambiguous. As with this example, the only thing that a student could be expected to make any sense of is finding an invertible matrix $P$ such that $P^T A P = D$ is diagonal. The diagonal entries will agree with the eigenvalues as far as $\pm$ signs or zero, that is Sylvester's Law of Inertia. I asked for references about one method for this at http://math.stackexchange.com/questions/1388421/reference-for-linear-algebra-books-that-teach-reverse-hermite-method-for-symmetr The method will give $P$ rational and $\det P = 1.$ – Will Jagy Jun 23 '17 at 21:29
  • 1
    @WillJagy I understand. Thank you for explaining this to me. – José Carlos Santos Jun 23 '17 at 21:32
0

To put this another way: you've found an invertible matrix $P_1$ such that $$ A = P_1^TBP_1 $$ (here, $P_1 = [v_1\;v_2\;v_3\;v_4]$). Now, consider the submatrix $$ B_0 = \pmatrix{-4&3&-2\\3&-1&1\\-2&1&3} $$ we can find a matrix $P_2$ such that $B_0 = P_2^TCP_2$, where $$ C = \pmatrix{\pm 1&0&0\\0&*&*\\0&*&*} $$ All together, we have $$ A = P_1^TBP_1 = P_1^T \pmatrix{1&0\\0&B_0} P_1 = P_1^T \pmatrix{1&0\\0&P_2^TCP_2} P_1 \\ = P_1^T\pmatrix{1&0\\0&P_2}^T \pmatrix{1&0 \\ 0& C}\pmatrix{1&0\\0&P_2}P_1 \\ = \left[\pmatrix{1&0\\0&P_2}P_1\right]^T \pmatrix{1 \\ & \pm 1\\ &&*&*\\&&*&*}\left[\pmatrix{1&0\\0&P_2}P_1\right] $$ We can continue this pattern inductively.

Ben Grossmann
  • 225,327
0

The method of repeated completing squares also leads, by nature, to rational entries in this case. However, that is not the end of the story, as the given form is $SL_4 \mathbb Z$ equivalent to a diagonal form. In brief, $$ (w + 2x+z)^2 + (x-2y+z)^2 - (9x-9y+13z)^2 + 19 (2x-2y+3z)^2 = w^2 - y^2 + 4z^2 + 4wx +6xy +2wz +2yz $$

$$ A = \left( \begin{array}{rrrr} 1 & 2 & 0 & 1 \\ 2 & 0 & 3 & 0 \\ 0 & 3 & -1 & 1 \\ 1 & 0 & 1 & 4 \end{array} \right) $$

$$ Q = \left( \begin{array}{rrrr} 1 & 2 & 0 & 1 \\ 0 & 1 & -2 & 1 \\ 0 & 9 & -9 & 13 \\ 0 & 2 & -2 & 3 \end{array} \right) $$ and

$$ D = \left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 19 \end{array} \right) $$

The one-line formula above is just $$ Q^T D Q = A $$

As far as the order the question was asked, we take $$ P = Q^{-1} = \left( \begin{array}{rrrr} 1 & 2 & -6 & 25 \\ 0 & -1 & 4 & -17 \\ 0 & -1 & 1 & -4 \\ 0 & 0 & -2 & 9 \end{array} \right) $$ to get $$ P^T A P = D. $$ Indeed, $$ P^T = \left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 2 & -1 & -1 & 0 \\ -6 & 4 & 1 & -2 \\ 25 & -17 & -4 & 9 \end{array} \right) $$ and $$ \left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 2 & -1 & -1 & 0 \\ -6 & 4 & 1 & -2 \\ 25 & -17 & -4 & 9 \end{array} \right) \left( \begin{array}{rrrr} 1 & 2 & 0 & 1 \\ 2 & 0 & 3 & 0 \\ 0 & 3 & -1 & 1 \\ 1 & 0 & 1 & 4 \end{array} \right) \left( \begin{array}{rrrr} 1 & 2 & -6 & 25 \\ 0 & -1 & 4 & -17 \\ 0 & -1 & 1 & -4 \\ 0 & 0 & -2 & 9 \end{array} \right) = \left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 19 \end{array} \right) $$

Will Jagy
  • 139,541