5

How does one prove that the class number of $\mathbb{Z}[\zeta_3]$ is $1$?

Jason Smith
  • 1,095

1 Answers1

19

Here's a nice geometric argument, which you can find essentially in Klein's lecture on Ideal Numbers (Lecture VIII in Lectures of Mathematics, by Felix Klein, AMS Chelsea Publishing, AMS, 2000).

Consider the lattice $\mathbb{Z}[\zeta_3]$ in $\mathbb{C}$ ($\zeta_3 = \frac{-1+\sqrt{-3}}{2}$). Given $a,b\in\mathbb{Z}[\zeta_3]$, $a\neq 0$. Consider the points in the lattice of the form $(q_1+q_2\zeta_3)a$, and use them to tessellate the complex plane. Then locate $b$, and the closest corner of one of the squares to $b$, $qa$. Then let $r=b-qa$.

Here is a picture which is slightly off, since my lattice here is $\mathbb{Z}[i]$, not $\mathbb{Z}[\zeta_3]$, but it should give you an idea; it's taken from the slides for a talk I gave some years ago. It's a bit hard to see, but the small dots are the lattice points; the big dots represent the $\mathbb{Z}[\zeta_3]$ multiples of $a$, with $a$ the first large dot to the right of the one labeled $0$ and above the horizontal line. (Well, as I said,t he small dots are really in the position of the lattice points of $\mathbb{Z}[i]$, but you get the idea, I hope). The three labeled dots above zero are (counterclockwise) $a$, $(1+\zeta_3)a$, and $\zeta_3 a$. The dot corresponding to $b$ is circled in red. The blue dot is $qa$, the blue arrow is the vector corresponding to $qa$, and the green arrow is the vector corresponding to $r = b-qa$. (The "1" at the very bottom of the picture is the page number, so ignore it...)

$\hskip 0.7in$ 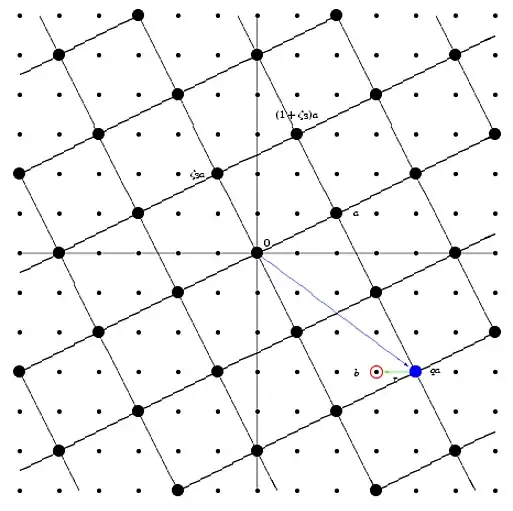enter image description here

How big can $r$ be? The tessellation is by parallelograms whose sides have length $|a|$ and $|\zeta_3 a|=|a|$, so the furthest that $b$ can be from the corner it is closest to is $\frac{|a|\sqrt{2}}{2}$. That is, $|r|\leq\frac{|a|\sqrt{2}}{2}\lt|a|$. From this it follows that $0\leq N(r)\lt N(a)$.

Thus, for all $a,b\in\mathbb{Z}[\zeta_3]$, there exists $q,r\in\mathbb{Z}[\zeta_3]$ such that $b = qa+r$, and $0\leq N(r)\lt N(a)$. So $N$ is a Euclidean function on $\mathbb{Z}[\zeta_3]$, the latter is Euclidean, hence a PID, hence the class number is $1$.

The same geometric argument can be used to show that $\mathbb{Z}[i]$ and $\mathbb{Z}[\sqrt{-2}]$ are Euclidean, but it breaks down when you get to $\mathbb{Z}[\sqrt{-5}]$, because the size of the rectangles now allows the distance from $b$ to a corner to be larger than the length of $a$ (good thing, too, since $\mathbb{Z}[\sqrt{-5}]$ is not a UFD).

no lemon no melon
  • 2,129
Arturo Magidin
  • 398,050
  • 1
    Thanks, that helps a lot. Are you basically giving a geometric argument for the Minkowski bound which can be used to show that it is Euclidean. – Jason Smith Feb 22 '11 at 16:59
  • You can go all the way to (-)11, among the Heegner numbers, in this way. Using a radicand whose absolute value is $\equiv 3\bmod 4$ allows the "unit-cell" areas to be rendered as triangles instead of rectangles, so the area does not get too big as quickly. – Oscar Lanzi Jul 09 '20 at 14:43
  • @Arturo is $r$ the same in $(r+s\zeta_3)a$ and $r=b-qa$? – no lemon no melon Feb 23 '21 at 09:22
  • @nolemonnomelon We are trying to show that $q$ and $r$ exist, satisfying $b=qa+r$ andn $N(r)\lt N(a)$. We find the closest lattice point, necessarily of the form $qa$, to $b$. Then we define $r$ to be equal to $b-qa$ to ensure that $b=qa+r$; then we verify that the choice, and how the lattice is defined, ensures that $N(r)\lt N(a)$. – Arturo Magidin Feb 23 '21 at 16:29
  • @Arturo thanks! Got it! $qa$ is defined to be of the form $(r+s\zeta_3) a$ so I was wondering if $r$ was the same as $r= b-qa$ but maybe that was just a coincidence, maybe it was more like $(r_1+s_1\zeta_3)a$. Anyhow, I read the Felix Klein part and what about the angles? How can I convince myself that $|r|< \frac{\sqrt{2}|a|}{2}$, I mean sure since the length of both sides of the parallelogram are |a| if the angles are $90^\circ$, but what if we didn’t have a square? I can guess it intuitively, I was wondering if you had a nice demonstration of this – no lemon no melon Feb 23 '21 at 18:54
  • @nolemonnomelon: The distance is still bounded by distance to the corners; it's not a rectangle here, since you start with $0$, $1$, $\zeta_3$ and $1+\zeta_3$; you get a parallelogram all of whose sides are length $1$, since $|\zeta_3|=1$. The sides are still $|a|$, because multiplication by $a$ performs a dilation by a factor of $|a|$ and a rotation by $\mathrm{arg}(a)$; the first makes the parallelogram have sides of length $|a|$, the latter does not change the sides, and then you are just tessellating. – Arturo Magidin Feb 23 '21 at 19:03
  • How does it follow from $|r|\leq |a|$ that $N(r)<N(a)$? – cansomeonehelpmeout Oct 23 '23 at 17:10
  • @cansomeonehelpmeout Please read carefully. What is proven is that $|r|$ is strictly less than $|a|$, not less than or equal. Since here the norm is the Euclidean distance, $|r|\lt|a|$ implies $N(r)\lt N(a)$. – Arturo Magidin Oct 23 '23 at 17:17
  • $N(a+b\zeta)=a^2+b^2$, and not $a^2-ab+b^2$? – cansomeonehelpmeout Oct 23 '23 at 18:24
  • @cansomeonehelpmeout Which part of "the norm is the Euclidean distance" was unclear? It's not the algebraic norm function. It's the Euclidean distance in the complex plane. – Arturo Magidin Oct 23 '23 at 18:24