23

Question

How can I find the sum of the series $$S=a^{\sqrt{1}}+a^{\sqrt{2} }+a^{\sqrt{3}}+a^{\sqrt{4}}+...$$ under the condition $0 \leq a < 1$

Short version

I think the sum of the series should be about $$S=\frac{2} {(\ln a)^2}+c$$ where c is a correction term. So the question is how should I find the value of $c$?

Long version

My approach so far:

The sum can be restated in terms of $y=f(x)$ where $$y_1=\sum_{n=1}^{\left \lfloor{x}\right \rfloor}a^{\sqrt{n}}$$ so the problem now is to find the limiting value of $y_1$ as $x \rightarrow \infty$. Instead of finding the limit of $y_1(x)$ as defined now, I tried to find another function with a similar growth rate: $$\frac{\mathrm{d} y_2}{\mathrm{d} x}=a^{\sqrt{x}}$$ $${\textrm{i.e. }} y_2=\int a^{\sqrt{x}}{\mathrm{d} x} $$ which on solving yields $$y_2=\frac{2 \sqrt{x} a^{\sqrt{x}}} {\ln a} - \frac{2a^{\sqrt{x}}} {(\ln a)^2}+\frac{2} {(\ln a)^2}$$ where the constant of integration is so chosen to make the curve pass through the origin.

Now plotting both these functions on Desmos 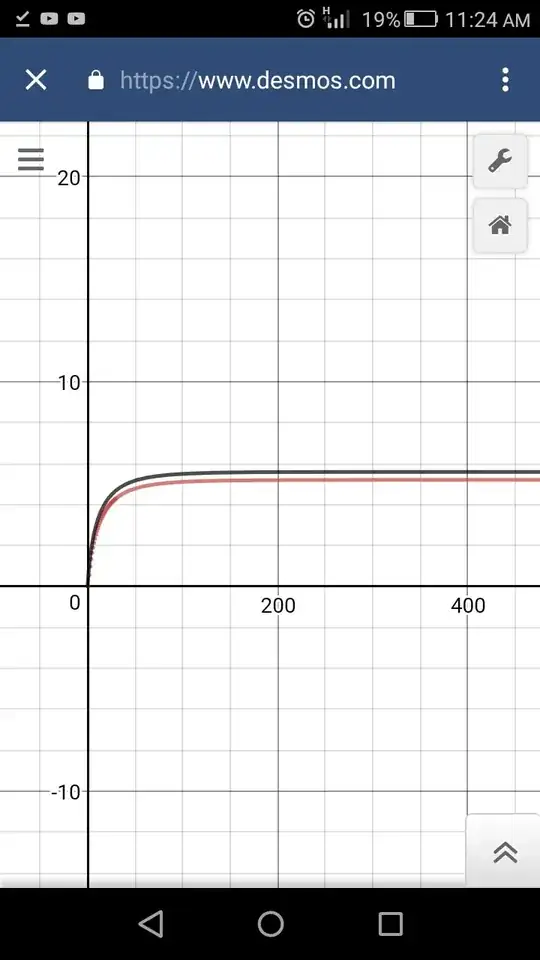screenshot shows that $y_1$ and $y_2$ resemble each other closely. However $y_2$ has faster initial growth, and therefore it's limiting value is slightly larger than the limiting value of $y_1$ which is what I'm after. The limiting value of $y_2$ is $$S_2=\lim_{x \rightarrow \infty}{y_2(x)} =\frac{2} {(\ln a)^2}$$ Therefore, I think the actual sum of the original series should be: $$S=\frac{2} {(\ln a)^2}+c$$ where $c$ is a correction term, possibly depending on $a$.

I'm stuck on how to find the correction term $c$ and what it's form should be. Is my approach so far correct? Any help would be appreciated.

curious
  • 243
  • 2
    You probably want to start from https://en.wikipedia.org/wiki/Euler–Maclaurin_formula; that's the first thing that springs to mind for a sum like this... – Steven Stadnicki May 19 '17 at 06:08
  • I'm not familiar with the Euler-Maclaurin formula, although it seems suitable for my problem. I was hoping for a more elementary solution. I'll try and look into this formula. – curious May 19 '17 at 06:14
  • 2
    I doubt there is any elementary solution, if one apply Abel-Plana formula to the sum, one obtain following integral representation of the sum:

    $$S = \frac{2}{(\log a)^2} - \frac12 + \frac1\pi \int_0^\infty \frac{e^{-\beta\sqrt{t}}\sin(\beta\sqrt{t})}{e^t-1}dt \quad\text{ where }\quad \beta = \frac{-\log a}{2\sqrt{\pi}}$$

    The last integral doesn't looks like one that is expressible in elementary functions.

     – achille hui May 19 '17 at 07:41
  • @achille Yeah, I guess it is unlikely that an elementary solution exists. – curious May 19 '17 at 08:05
  • 2
    Euler-Maclaurin formula does yield that, with $s = -\log a$, $$ \sum_{n=1}^{\infty} e^{-s\sqrt{n}} = \frac{1}{s} - \frac{1}{2} + \frac{\zeta(3/2)}{4\pi}s + o(s) $$ as $s \downarrow 0$. That said, $c$ is not just a constant but a function of $a$ which converges to $-\frac{1}{2}$ as $a \uparrow 1$. Notice that this is also consistent with achille hui's computation, as $$ \lim_{s \to 0} \frac{1}{s} \int_{0}^{\infty} \frac{e^{-\beta\sqrt{t}} \sin(\beta\sqrt{t})}{e^t - 1} , dt = \frac{1}{2\sqrt{\pi}} \int_{0}^{\infty} \frac{\sqrt{t}}{e^t - 1} , dt = \frac{1}{4}\zeta(3/2). $$ – Sangchul Lee May 19 '17 at 08:06
  • @Lee I see, thanks. What does the arrows mean? I know that it is used to indicate large integers, but I dont know the specifics. I was trying to solve random problems in my leisure, I guess I came up with a more difficult problem than I anticipated. – curious May 19 '17 at 08:14
  • $a\uparrow 1$ is the same as $a \to 1^-$ (limit from the left) and similarly $s \downarrow 0$ is the same is $s \to 0^+$ (limit from the right). Arrows are so universal that every part of mathematics has its own vernacular using arrow notation. In this case, it's not a fancy thing and simply denotes one-sided limits. – Sangchul Lee May 19 '17 at 08:26
  • Oh, I confused them with Knuth notation – curious May 19 '17 at 08:31
  • 1
    @SangchulLee Your computation suggests a first term proportional to $(\log a)^{-1}$ rather than $(\log a)^{-2}$ as both OP and achille get? – Steven Stadnicki May 19 '17 at 15:56
  • 1
    @StevenStadnicki, Thank you for pointing out the typo. It should be $$ \sum_{n=1}^{\infty} e^{-s\sqrt{n}} = \frac{1}{s^2} - \frac{1}{2} + \frac{\zeta(3/2)}{4\pi}s + o(s). $$ – Sangchul Lee May 19 '17 at 23:35
  • 1
    I think some one should post an official answer to this question, there's been such a nice discussion in the comments – curious May 20 '17 at 05:59
  • Applying the Euler-Maclaurin formula, we find that$$S=\int_t^\infty a^{\sqrt x}~\mathrm dx-\frac{a^{\sqrt t}}2-\sum_{k=1}^\infty\frac{B_{2k}}{(2k)!}f^{2k-1}(t)+R$$Where $R$ is the remainder term as given in the link (as $p\to\infty$). From here we can deduce that as $t\to0^+$,$$S=\frac2{(\ln a)^2}-\frac12+\text{mess}$$Where one could probably work out what the messy part is with some elbow grease. – Simply Beautiful Art Jun 29 '17 at 17:22

1 Answers1

8

We can keep going on the line of the comments for something that converges as close as necessary, starting from $$ S = \frac{2}{(\log a)^2} - \frac12 + \frac1\pi \int_0^\infty \frac{e^{-\beta\sqrt{t}}\sin(\beta\sqrt{t})}{e^t-1}dt \quad\text{ where }\quad \beta = \frac{-\log a}{2\sqrt{\pi}} $$ as given by @achille hui in the comments. We can try and get a form for the integral, $$ I(\beta) = \int_0^\infty \frac{e^{-\beta\sqrt{t}}\sin(\beta\sqrt{t})}{e^t-1}dt $$ by taking a Mellin transform of the integrand with respect to $\beta$ we get $$ \int_0^\infty \beta^{s-1}I(\beta)\; d\beta = \Gamma(s)\sin\left(\frac{\pi s}{4}\right)\int_0^\infty \frac{(2t)^{-s/2}}{e^t-1} \; dt $$ this is then $$ \int_0^\infty \beta^{s-1}I(\beta)\; d\beta = 2^{-s/2}\Gamma(s)\sin\left(\frac{\pi s}{4}\right)\Gamma\left(1-\frac{s}{2}\right)\text{Li}_{1-\frac{s}{2}}(1) $$ we want to take the inverse Mellin transform of both sides to get $I(\beta)$ but it's not trivial to do this for the RHS, so invoke the Ramanujan Master Theorem, that the Mellin transform of $I(\beta)$ is written $$ \int_0^\infty \beta^{s-1}I(\beta)\; d\beta = \Gamma(s)\phi(-s) $$ such that $$ I(\beta)=\sum_{n=0}^\infty \frac{(-1)^n}{n!}\phi(n)\beta^n $$ then we have $$ \phi(s)= \sin\left(\frac{-\pi s}{4}\right)2^{s/2}\Gamma\left(1+\frac{s}{2}\right)\text{Li}_{1+\frac{s}{2}}(1) $$ and using $$ \text{Li}_{1+\frac{s}{2}}(1) = \zeta\left(1+\frac{s}{2}\right), \;\; s>0 $$ we can write $$ I(\beta)=\sum_{n=0}^\infty \frac{2^{n/2}}{n!}\sin\left(\frac{-\pi n}{4}\right)\Gamma\left(1+\frac{n}{2}\right)\zeta\left(1+\frac{n}{2}\right)\left(\frac{\log{a}}{2\sqrt{\pi}}\right)^n $$ finally $$ \sum_{n=1}^\infty a^{\sqrt{n}}=\frac{2}{(\log a)^2} - \frac12 -\frac{\log(a)\zeta\left(\frac{3}{2}\right)}{4\pi} -\frac{\log(a)^2\zeta\left(2\right)}{4\pi^2}-\frac{\log(a)^3\zeta\left(\frac{5}{2}\right)}{32\pi^2}+\frac{\log(a)^5\zeta\left(\frac{7}{2}\right)}{512\pi^3}+\cdots $$

Benedict W. J. Irwin
  • 4,321