Graph-theoretically, a map is a cubic graph ${\displaystyle \Gamma }$ with edges colored blue, yellow, red such that: $\Gamma$ is connected, every vertex is incident to one edge of each color, and cycles of edges not colored blue, have length 4.
So I wonder whether graphs $\Gamma_\mathfrak B$ with the following properties
- bicubic
- planar
- with faces having 4 and 6 vertices only
- where the squares are separated (this is class 4 from this post here)
can represents maps?
Planarity would guarantee a 3-edge coloring via the 4-color theorem. I checked the planar drawing below which I thought it should be the truncated octahedron and it didn't work. Reading further on Wikipedia:
Note that $\Gamma$ is the flag graph or graph encoded map (GEM) of the map.
My question rephrased is: When are graphs $\Gamma_\mathfrak B$ gems?
EDIT Looks like I've taken the wrong graph
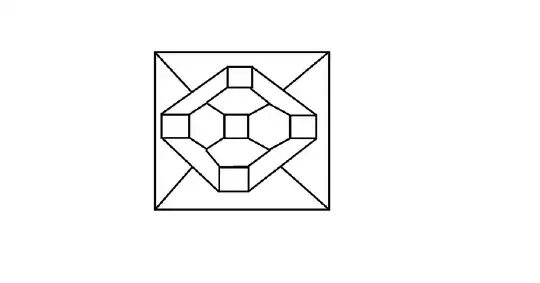 which is not the truncated octaeder, but a chamfered cube.
which is not the truncated octaeder, but a chamfered cube.