$\sin(1/x)$ space with a line is not locally path connected?

Question

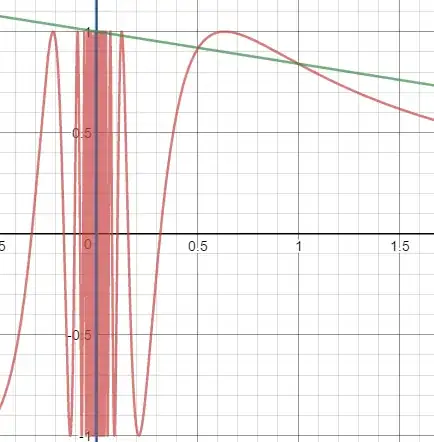
Let $X = \text{ $\sin(1/x)$ space } \cup \text { line from $(0,1)$ to $(\frac{1}{2 \pi}, 0$})$,

Where $$\sin(1/x) \text { space }= \{(0,y) : y \in [-1,1] \cup \{(x, \sin(1/x)) : x \in (0, \frac{1}{2 \pi}]\}$$

Show that $X$ is path connected but not locally path connected.

The definition of locally path connected: $X$ is locally path connected if, for each $x \in X$ and every open neighborhood $U$ of $x$, there is an open $V$ with $x \in V \subseteq U$ such that any two points in $V$ can be jointed by a path in $U$.

Path connected is simple to prove, but I can't see how this isn't locally path connected.

Anyone have any ideas?

Where did you get stuck when you looked at the definition of locally path connected and attempted to prove it? — Lee Mosher, May 16 '17 at 13:27
@Clayton But if the space is path connected, how can $(0,-1)$ have no path to other points on the graph? — Oliver G, May 16 '17 at 13:31
@SEWillB How does $(0,-1)$ not satisfy the definition of locally path connected? — Oliver G, May 16 '17 at 13:34
Your question doesn't make sense: all path-connected spaces are locally path-connected, so no such $X$ can exist. (Also, what does "$\sin(1/x)$ space" mean?) — TonyK, May 16 '17 at 13:38
@TonyK The definition of that space is provided in the question. — Oliver G, May 16 '17 at 13:38
@TonyK How does path-connected imply locally path connected? — Oliver G, May 16 '17 at 13:41
@TonyK: Of course not. Why would you think that? Path-connectedness and local path-connectedness are mostly orthogonal properties (and the Warsaw circle is probably the simplest example of that). — tomasz, May 16 '17 at 14:01
@SEWillB: No, it doesn't. I think the intended space is supposed to include $-1\leq y\leq 1$ on the $y$-axis, but as written, it has only two points, only one of which is connected by a line. — Clayton, May 16 '17 at 14:05
@Clayton oh yeah you're correct; I must have read those ${, }$ brackets as $[, ]$ brackets. But I presume this is what is meant. Otherwise I'll have to delete my answer :( — SEWillB, May 16 '17 at 14:07
@SEWillB: I'm sure that is the intention, it just hasn't been written. :) — Clayton, May 16 '17 at 14:10
@OliverG: Sorry! I was mistaken about path-connected implying locally path-connected. Here is a stackexchange question on this very subject. — TonyK, May 16 '17 at 14:28

score 1 · Accepted Answer · answered May 16 '17 at 13:54

It is probably easiest to show that the point $(0, 0)$ doesn't satisfy the property of being locally path connected. The picture below shows the space in question: (ignore the left of the y-axis)

Pick an open ball of radius $R$ about $(0,0)$ with $R$ small enough that the ball doesn't intersect the green line. Denote this $B((0,0), R)$. Given any open subset $V$ of $B((0,0), R)$ we must have an open ball of radius $r \le R$ with $B((0,0), r) \subset V$.

If we can show that these spaces are not path connected then we're done. However it is obviously the case that these spaces are not path connected. If we could join up the $\sin(1/x) \text{-space}$ to the $y$-axis by a continuous path all inside $B((0,0), r)$; then we could certainly join up simply the $\sin(1/x) \text{-space}$ to the $y$-axis not necessarily constrained to the open ball $B((0,0), r)$.
However this cannot be done (this is a standard example of non-path connected space that is a connected space - see 'topologists sine curve'). But if you need help with this just ask. Hope this helps!

$\sin(1/x)$ space with a line is not locally path connected?

1 Answers1