59

The Section on Covering Maps in John Lee's book "Introduction to Smooth Manifolds" starts like this:

Suppose $\tilde{X}$ and $X$ are topological spaces. A map $\pi : \tilde{X} \to X$ is called a covering map if $\tilde{X}$ is path-connected and locally path connected, ... (etc).

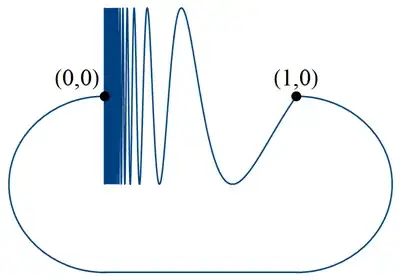
I hope this question is not too dumb, but how can a space be path connected, but not locally path connected ?

EDIT: I am aware of spaces that are locally path-connected yet not path-connected, but I cannot come up with a space that is path - connected yet not locally path connected.

harlekin
  • 8,740
  • 23
    See here – David Mitra Apr 22 '12 at 19:51
  • This is a great comment. – Kerry Apr 22 '12 at 19:53
  • @DavidMitra: WOW .. Topology always amazes me, there are so many things that I learn from these counterexamples .. many thanks for pointing me to the link!! – harlekin Apr 22 '12 at 19:54
  • 3
    I am to unsure to answer: "because the path witnessing path connectedness might have to pass though a specific point (or be otherwise constrained)". There are other examples. From Steen and Seebach's Counterexamples in Topology: The Alexandroff Square (ex 101), The Extended Topologist's Sine Curve (ex 118), The Closed Infinite Broom (ex. 120), and the Integer Broom (ex 121). – David Mitra Apr 22 '12 at 20:01
  • For another example (a subspace of $\mathbb R^2$ which is path-connected and locally connected but not locally path-connected, due to M. Shimrat) see https://math.stackexchange.com/questions/1492772/connected-locally-connected-path-connected-but-not-locally-path-connected-subs – bof Apr 01 '23 at 02:05

3 Answers3

85

One counterexample is a variant on the famous topologist's sine curve.

Consider the graph of $y = \sin(\pi/x)$ for $0<x<1$, together with a closed arc from the point $(1,0)$ to $(0,0)$:

enter image description here

This space is obviously path-connected, but it is not locally path-connected (or even locally connected) at the point $(0,0)$.

Jim Belk
  • 49,278
7

You should consider the opposite question, that how a space could be locally path connected, but not path connected. And this should be simple: consider the union of two open disks.

Kerry
  • 2,286
  • I think harlekin's point, then, is why both hypotheses are being made. Why not just say $\widetilde{X}$ is locally path-connected? – KCd Apr 22 '12 at 19:48
  • Thanks for your comment! I have added my post to clarify what confuses me - in my topology course I have seen spaces that are locally path-connected yet not path-connected, but what I have trouble with is coming up with a path-connected space that is not locally path-connected. Yet this is what Lee's opening part of the definition of a covering map suggests exists - I suppose .. – harlekin Apr 22 '12 at 19:49
  • 1
    $KCd: I understand. If I am not being mistaken I think Hatcher's book has some discussion relevant to this. – Kerry Apr 22 '12 at 19:51
  • Ok I shall have a look at Hatcher's book as well, I am currently reading about the Comb space, as suggested by David, but thanks a lot for your suggestion ! – harlekin Apr 22 '12 at 19:55
  • On page 63 he commented that if the space is both path-connected and locally path-connected, then components are the same as path components, which simplifies his discussion on the Galois correspondence on the covering space. – Kerry Apr 22 '12 at 19:59
4

$\pi$-Base, an online version of Steen and Seebach's Counterexamples in Topology, lists the following spaces as path-connected but not locally path-connected. You can view the search result for more information about these spaces.

Alexandroff Square

Extended Topologist’s Sine Curve

The Closed Infinite Broom

The Integer Broom

Steven Clontz
  • 5,719
Austin Mohr
  • 25,662