4

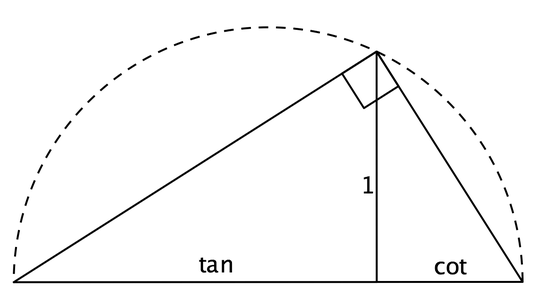
So I was wandering through Wikipedia, as you do, when I stumbled across this beaut:

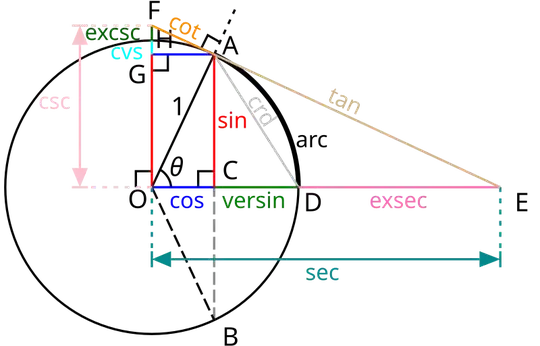
a geometric diagram of the trigonometric functions

Long story short, this "triangle of measures" has been occupying my time for a while now. My goal is this: given only the ratio between any two (straight) named lengths in the diagram, or between any one length and the radius of the relevant circle (the length given as "1" in the diagram), construct the entire triangle with straightedge and compass.

So far, I've proven the cases with radius and any other length; with any two of sine, versine or chord; with sine and cosine; with sine and tangent; with secant and tangent; with secant and exsecant, and with secant and cosecant. The co-forms are analogous and trivial to prove from these.

I have also discovered that given tangent and cotangent I can use a guess-and-adjust construction to find the height necessary to make cot+tan a hypotenuse, and thus the radius, but I can't find a strict straightedge-and-compass construction.

I am also aware that it may well be impossible to use certain pairs to construct the whole triangle of measures, but my disproving abilities are far behind my proving abilities. Any proofs or disproofs would be appreciated.

Edit I: Thanks to Aretino, I have learned a compass-and-straightedge construction from only cotangent and tangent. This led to an analogous construction from cosine and secant, as well as a guess-and-adjust one for sine and secant (And their analogous co-forms, obviously).

Edit II: After some thinking, the guess-and-adjust construction from sine and secant has yielded to the compass and straightedge! First, construct a semicircle with a diameter of the secant. Second, construct a perpendicular anywhere along the line of the secant and mark off the sine along the perpendicular. Third, construct a perpendicular from the free end of the sine on the original perpendicular; call this the parallel. Where the parallel hits the semicircle (provided the semicircle and the sine are on the same side, this will happen twice) will be a possible point for the right angle between tangent and radius. Drop the sine from either point to the secant and then construct the tangent and radius. From there, the rest of the triangle is constructable.

No Name
  • 741
  • 5
  • 13
  • If anyone would like to see my proofs for the constructions I did figure out, please let me know. However, I am going to bed right now, so it will be a while before I post again. – No Name Apr 27 '17 at 04:10
  • You may find the following relevant: Representing the multiplication of two numbers on the real line and Constructing the reciprocal of a segment. – dxiv Apr 27 '17 at 04:19
  • If this was the only missing pair of interest, you should accept Aretino's answer by clicking the check mark. If there is still something left to the question, please let us know what it is. –  Apr 28 '17 at 04:23
  • @Rahul As I state in the second paragraph, I am curious about any two lengths. The list of pairs I'm confident in, which I give in the following paragraphs (including the first Edit), is less than half of that total. – No Name Apr 28 '17 at 05:01
  • I see, you're looking for all $\binom{12}2$ constructions... Might be useful to add an answer that spells out the symmetries that reduce the number of cases, and to keep track of the ones already known to you. –  Apr 28 '17 at 05:19
  • P.S. I tried writing an answer just covering the pairs with $\sin$ (only 11 out of 55!) and still got tired and gave up halfway through. This question is asking for a lot. –  Apr 28 '17 at 05:54

1 Answers1

2

As $\tan\theta\cdot\cot\theta=1$, to construct the radius you can just draw a circle of diameter $\tan\theta+\cot\theta$ and intersect it with a perpendicular, as shown in the diagram below. You get then a right angled triangle, whose altitude, by the intersecting chords theorem, is $1$.

enter image description here

Intelligenti pauca
  • 50,470
  • 4
  • 42
  • 77