4

Given a (possibly) overdetermined linear system $Ax=b$, where

$A$ is full rank and $A \in \mathbb{R}^{m \times n}, \quad m \ge n$

Does the least squares method provide an exact solution (instead of an approximation) if and only if $m=n$ (the system is square and well-determined)?

In other words can an overdetermined full rank system have an exact solution? If yes, when and how can you predict it?

plasmacel
  • 1,252
  • 2
    An overdetermined system(by which I mean, a system with more equations than unknowns) can certainly have an exact solution,e.g., $x+y=3$, $x-y=1$, $7x+8y=22$has the solution $(2,1)$. I think it's easier to just solve the system and see, than it is to try to predict. – Gerry Myerson Apr 21 '17 at 12:39
  • Yeah, I updated my question. I'm actually interested in the prediction whether an exact solution exist. Most sources say that such systems generally have no exact solution, but they don't mention when do they have. – plasmacel Apr 21 '17 at 12:44
  • They do when they do, there may not be much more you can say. – Gerry Myerson Apr 21 '17 at 12:44
  • A full rank overdetermined system has no solution. For existence of a solution, it must be rank deficient. –  Apr 21 '17 at 13:31
  • @YvesDaoust Do you mean a full rank overdetermined system has no exact solution (only an approximation)? – plasmacel Apr 21 '17 at 13:34
  • Such a system has no solution, full stop. If you want, you can find values that approximately satisfy the equations. But you can't have an approximation to a solution that doesn't exist. –  Apr 21 '17 at 13:36
  • @YvesDaoust Well, then my presumption is right. An $m \times n$ full rank system has a solution iff $m=n$. It has infinitely many solutions if $m<n$ (underdetermined system). Finally if $m>n$ (overdetermined system) then it has no solution and the best you can do is finding a best fit approximate solution using least squares method. – plasmacel Apr 21 '17 at 13:46
  • 1
    Other approximate solutions can be found using different criteria than the least squares. –  Apr 21 '17 at 13:47
  • @YvesDaoust Thanks, you helped to clear some things up. – plasmacel Apr 21 '17 at 13:54
  • 1
    @Yves, maybe I don't understand what "full rank" means. In the example in my first comment, $A$ is $3\times2$, so the biggest rank it can possibly have is 2, and it does have rank 2. Doesn't that make it full rank? – Gerry Myerson Apr 22 '17 at 13:37
  • @GerryMyerson You are right, your $3 \times 2$ example has rank $2$ which makes it full rank and it definitely does have a solution. However then in this case I'm confused again. – plasmacel Apr 22 '17 at 16:43

1 Answers1

5

Problem statement

Start with the matrix $$ \mathbf{A} \in\mathbb{C}^{m\times n}_{\rho}, \quad m > n. $$ and the data vector $b\in\mathbb{C}^{m}$. Classify the solution of the linear system $$ \mathbf{A} x = b $$

Unique solution, exact: $\lVert \mathbf{A}x - b\rVert = \mathbf{0}$

The data vector $b$ is entirely within the column space of $\mathbf{A}$: $$ \color{blue}{b} \in \color{blue}{\mathcal{R} \left( \mathbf{A} \right)} $$ Example: $$ \begin{align} % \mathbf{A} x &= b\\ % \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right] \left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ \end{array} \right] &= \left[ \begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \right] % \end{align} $$ Exact solution: $$ \left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ \end{array} \right] = \left[ \begin{array}{c} 1 \\ 0 \\ 0 \\ \end{array} \right] $$ There are no restrictions on matrix shape or rank. The touchstone is whether the data is in the $\color{blue}{range}$ space.

Geometric view:

• If the data vector has a $\color{red}{null}$ space component, there is no direct solution, and we must use least squares.

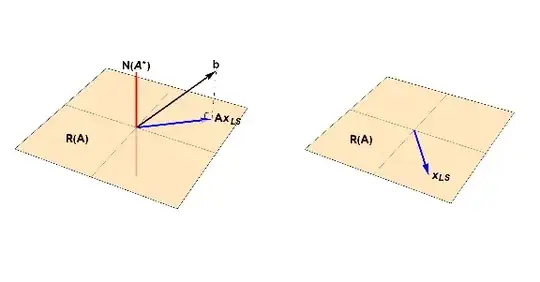
• If the data vector is in the column space, an exact solution exists; there is a direct solution. geometric view

Unique solution, not exact: $\lVert \mathbf{A}x - b\rVert > 0$

The data vector has components in both the $\color{blue}{range}$ and $\color{red}{null}$ spaces: $$ b = \color{blue}{b_{\mathcal{R}}} + \color{red}{b_{\mathcal{N}}} $$ The data vector cannot be expressed entirely in terms of combinations of the columns of the matrix $\mathbf{A}.$ The method of least squares is used to find the best approximation. This is the orthogonal projection of the data vector onto $\color{blue}{\mathcal{R} \left( \mathbf{A} \right)}$; the "shadow" of the data vector. In one of the follow on posts mentioned below, we see that the sum of the squares of the residual errors measures the amount of the data vector in $\color{red}{\mathcal{N} \left( \mathbf{A}^{*} \right)}$. The least squares solution is $$ \color{blue}{x_{LS}} = \color{blue}{\mathbf{A}^{+}b} $$

Infinite solutions, not exact: $\lVert \mathbf{A}x - b\rVert > 0$

The posts mentioned below explore this issue. The upshot is that $\color{red}{\mathcal{N} \left( \mathbf{A} \right)}$ is not trivial. The least squares solution is the affine space $$ x_{LS} = \color{blue}{\mathbf{A}^{+}b} + \color{red} {\left( \mathbf{I}_{n} + \mathbf{A}^{+} \mathbf{A} \right) y}, \quad y\in\mathbb{C}^{n} $$

No solution When the data vector is in the $\color{red}{null}$ space, $$ b \in \color{red}{\mathcal{N} \left( \mathbf{A}^{*} \right)} $$ there is no least squares solution.

Explore Stack Exchange:

Looking at the data vector to classify existence and uniqueness: Query about the Moore Penrose pseudoinverse method

This post shows that the sum of the squares of the residual errors is the magnitude of the component of the data vector in the $\color{red}{null}$ space. How does the SVD solve the least squares problem?

For your post, you wanted to classify solution based on the data vector. Here is the classification scheme when the data vector is not known: What forms does the Moore-Penrose inverse take under systems with full rank, full column rank, and full row rank?, generalized inverse of a matrix and convergence for singular matrix

dantopa
  • 10,342
  • 1
    By $A^\star$ do you mean $(\overline{A})^T$ i.e. conjugate transpose of $A$? – Kumar Sep 29 '20 at 09:36
  • The adjoint matrix $\mathbf{A}^{}$ is the transpose of the complex conjugate of $\mathbf{A}$, which is also the complex conjugate of the transpose matrix: $\mathbf{A}^{} = \left(\bar{\mathbf{A}}\right)^{\mathrm{T}} = \overline{{\mathbf{A}}^\mathrm{T}}$ – dantopa Oct 06 '20 at 04:30
  • I am still doubtful that your example has a unique solution as it violates Rouché–Capelli theorem. – Kumar Apr 13 '21 at 11:44