8

There are several beautifully written posts on stackexchange about duality. For example:

This post on Quora was quite good. It maps $f(x)$ (to be minimized) as a function of $g(x)$ the constraint (i.e. a function of a function), something no one else does, and garners some interesting graphic insights with this trick.

This post on Science4All illustrates the ying and yang of feasible and dual feasible sets.

This Youtube video explains the role of the dual vector in the cross product.

But something is still not clicking for me!!

I want to understand what Gilbert Strang means when he says, explaining the Theorem of the Alternative in Chap. 8 of his book Linear Algebra and Its Applications, that:

  • In $Ax = b$, the $b$ is in the column space of A, but
  • Adding a contraint to the equation $Ax = b$ means that the "$b$'s will no longer fill out a subspace. Instead, they fill a cone-shaped region"
  • If $b$ lies in this cone, there is a nonneative solution to $Ax = b$, otherwise not.
  • If $b$ lies outside the cone, there will be a separating hyperplane perpendicular to y which has the vector $b$ on one side and the whole cone on the other side.

By Fundamental Theorem of LA we show $Ax = b$ has a solution by showing $b$ is in the $C(A)$. But the Theorem of the Alternative offers an alternative way to determine solvability: $Ax = b$ has a solution or there is a $y$ such that $yA =0$ and $yb \ne 0$ ... "In the language of subspaces, either $b$ is in the column space, or it has a component sticking into the left nullspace. That component is the required $y$."

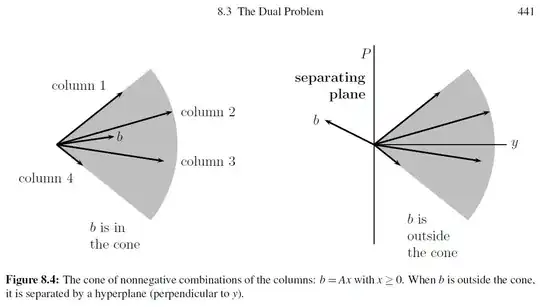
Image depicting relationship between separating hyperplane, y and b

Strang's comment continued: "Figure 8.4 shows a separating hyperplane which has the victor $b$ on one side and the whole cone on the other side. The plane consists of all vectors perpendicular to a fixed vector $y$. The angle between $y$ and $b$ is greater than 90 degrees, so $yb < 0$. The angle between $y$ and every column of $A$ is less than 90 degrees, so $yA \ge 0$. This is the alternative we are looking for. This theorem of the separating hyperplane is fundamental to mathematical economics"."

I realize I'm waving my hands big time here (or rather flailing like a beached dolphin), but I sense that Strang's diagram must be related somehow to this diagram Salman Khan offers of the respective roles of a matrix's row and null spaces in a solution to $Ax = b$.

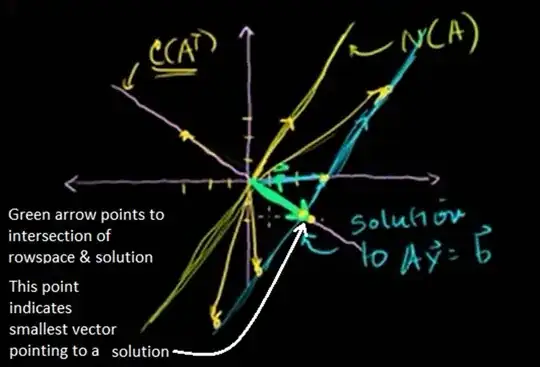
Image depicting respective roles of row and null spaces in solution to Ax = b

I see a relationship here that torments me. Maybe it is not meaningful, but one thing that makes me suspect these two diagrams (Strang's and Khan's) might be related is that in the Simplex Method, the dual tableau is the transpose of the primal tableau, much as in any matrix A, the rows defining the row space are the transpose of the columns defining the column space. And, of course, the nullspace is also orthogonal to the row space.

Can someone help me tie these concepts together?

John Strong
  • 181
  • You could include the link URLs as text for the benefit of the rest of us. We know how to copy-paste URLs into our browsers. –  Apr 14 '17 at 17:37
  • Anyway, I don't see what the theorem of the alternative (a.k.a. Farkas' lemma) has to do with all the links on duality you were trying to post. –  Apr 14 '17 at 17:42
  • 1
    I only loosely followed your bulleted summary of Strang (I have the book somewhere but I am lazy and don't want to look it up). I think teh following clarifications would be helpful: (i) I was quite confused about the precise meaning of "Adding a constraint to $Ax=b$," but now I am guessing Strang is talking about adding the inequality consraints $x_i\geq 0$ for $i \in {1, ..., n}$ is that correct? (ii) In the fourth bullet, there is a mysterious vector $y$ that shows up, what is that? – Michael Apr 14 '17 at 18:05
  • Great criticisms. I appreciate the rapid response, Raul and Michael. Just edited the post to address comments above. Will follow up later today. – John Strong Apr 14 '17 at 18:54
  • @JohnStrong : You give an edit about a vector $y$ in a "Theorem of the Alternative," but I do not think that vector $y$ is related to the Strang bullets. Strang is talking about a case where $b$ lies outside of a cone related to a matrix $A$ (perhaps that cone is the set of all points of the form $Ax$ such that $x_i \geq 0$ for all $i \in {1, ..., n}$). That vector $b$ might still be in $Col(A)$, but not in the cone. So your "Theorem of the alternative" does not apply. I think my two clarifications points (i), (ii) still need further followup. – Michael Apr 14 '17 at 19:29
  • I linked the URLs you added. However your first two links are identical, maybe there is a mistake there. –  Apr 15 '17 at 03:07

0 Answers0