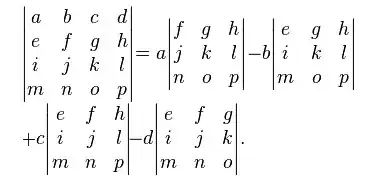Simplified method for symmetric matrices

Question

I am trying to find the determinant of the following $4\times 4$ symmetric matrix $A$ given as $$A= \begin{pmatrix} a & b & c & d \\ b & c & d & a \\ c & d & a & b \\ d & a & b & c \end{pmatrix}$$ Any solution and help would be appreciated. Thanks.

Answer 1

Some suggests a Row Reduction to create zeros in rows or columns, then use expansion by minors along that row/column. But I find this method easier to understand.

I hope it helps! :)

Answer 2

I'll explain the situation for $3 \times 3$ matrices, an you will have an idea of how it will work for larger matrices. It's a nice technique, though I don't know about the constant at the end.

The key:

Try to look for conditions on variables, that will make the determinant zero. That is, when we substitute these relations of variables into the determinant, maybe two rows become the same, or two columns become the same etc. Then, the remainder theorem will tell you that this determinant contains that relation, expressed as as a polynomial, as a factor.

I'll give you an example, by evaluating the $3 \times 3$ equivalent of this matrix: $$ \begin{bmatrix} a & b & c \\ b & c & a \\ c & a & b \end{bmatrix} $$

First of all, note that by doing $R_1 \to R_1 + R_2 + R_3$ : $$ \begin{bmatrix} a+b+c & a+b+c & a+b+c \\ b & c & a \\ c & a & b \end{bmatrix} $$

Now, if $a+b+c=0$, then the determinant will be zero. Hence, you see that $a+b+c$ is a factor of the given determinant.

Similarly, look at the original determinant. If $a=b=c$, then you can see that the determinant is zero. Hence, the determinant will be a multiple of $(a-b)^2 + (b-c)^2 + (c-a)^2$ also.

Now, since the degrees ($3$ and $3$) match,you can check that up to a constant, the determinant of the $3 \times 3$ case is $(a+b+c)((a-b)^2 + (b-c)^2 + (c-a)^2)$.

Similarly, in the four times four case:

1) Add all other rows to the first row, and note that if $a+b+c+d=0$ then the determinant is zero.

2) Similarly, if you let $c=a$ and $d=b$, then the first and third rows are the same, so you can check that $(c-a)^2 + (b-d)^2$ will divide the determinant.

3) Do $R_1 = R_1 -R_2 + R_3 -R_4$. This will give the first row as $[1,-1,1,-1] \times (a-b+c-d)$. Hence, if this quantity is zero, you get the determinant is zero, So this is another factor.

Finally, by comparing degrees, the product of these factors is up to a constant the determinant.

Last but not the least, since you want generalizations, I should compute this for a $5 \times 5$ determinant of that kind, and see where we can go.

So, the $5 \times 5$ determinant will look like: $$ \begin{bmatrix} a & b & c & d & e \\ b & c & d & e & a \\ c & d & e & a & b \\ d & e & a & b & c \\ e & a & b & c & d \end{bmatrix} $$

A look at the above matrix should tell you at least the following. Unfortunately Wolfram is hanging when I try to figure out the answer, but I want you to check at least the following:

1 ) $a+b+c+d+e$ is a factor of the determinant.

2) If $a=b=c=d=e$, then the determinant is zero, so $\frac 12 \sum_{x\neq y, (x,y) \in \{ a,b,c,d,e\}^2} (x-y)^2$ is a divisor of the given polynomial.

If not completely solve the question, at least this technique sheds light on the manner in which you can possibly approach larger matrices of this kind.

This technique is immensely useful in evaluating many symmetric, or patterned determinants up to a constant, especially the Cauchy formula for determinants of the form $\frac{1}{X_i + Y_j}$.