2

The problem is simple

"Find the splitting field of $x^3+2x^2-5x+1$"

Yeah because it's too simple that I don't know how explicit should the splitting field be. I mean we take 3 roots and let the desired field be the field generated by them. But can we find it more explicitly?

Thank you

T C
  • 2,563
  • No, not more explicit. Do find the three roots and take the field generated by them and the basis field (is it $;\Bbb Q;$ or something else?) – DonAntonio Mar 28 '17 at 08:12
  • 1
    The discriminant of your polynomial is $D=361=19^2$ a square, so the Galois group is cyclic of order three. By Kronecker-Weber the splitting field is a subfield of a cyclotomic field. It doesn't take a genius to suspect that the conductor is $19$. Do you know Galois theory? If you do, then it shouldn't be too difficult to find the only cubic subfield of $\Bbb{Q}(e^{2\pi i/19})$. – Jyrki Lahtonen Mar 28 '17 at 10:31
  • 1
    Anyway, $\sigma:\zeta\mapsto \zeta^2$ gives the generator of $Gal(L/\Bbb{Q})$, $L=\Bbb{Q}(\zeta)$, $\zeta=e^{2\pi i/19}$. The cubic subfield $K$ is the fixed field of $\sigma^3$, so it contains the number $$\alpha=\sum_{j=0}^5\sigma^{3j}(\zeta)=2\big(\cos(2\pi/19)+\cos(16\pi/19)+\cos(14\pi/19)\big).$$ Therefore my guess is that the splitting field if $\Bbb{Q}(\alpha)$. – Jyrki Lahtonen Mar 28 '17 at 10:37
  • Judging from the approximate values it looks like $-1-\alpha$ is one of the zeros of your polynomial. Do check! – Jyrki Lahtonen Mar 28 '17 at 10:40
  • Most of the above was partly me showing off. Just from plotting the polynomial you can tell that it has three real zeros. Cardano's formula is the brute force method for finding the roots. You need a bit more to show that adjoining one gives you the others as well. Whenever we get a cubic cyclic extension of $\Bbb{Q}$ some trick like the one above will work (but Kronecker-Weber is too deep a theorem to get covered in a first course in Galois theory). – Jyrki Lahtonen Mar 28 '17 at 10:47
  • So we call x1, x2 and x3 3 roots, ok. Obviously the field generated by Q and 2 out of 3 is whay we want. But could it be a simple extension – T C Mar 28 '17 at 10:49
  • Yes, the discriminant test tells that one of the roots is enough. Any one will do. – Jyrki Lahtonen Mar 28 '17 at 10:50
  • O...k. i just learned about the existence of splitting field, so it's a little hard for me to understand. Thank you anyway – T C Mar 28 '17 at 10:51
  • That's ok. We all need to be at that point and learn to move forward, you'll do fine! I try to think of a more elementary way of seeing this. There is one, but it needs a bit of work :-) – Jyrki Lahtonen Mar 28 '17 at 10:53
  • Ok. Here is an elementary suggestion. Show that if $\beta$ is a zero of your polynomial then $\beta^2+3\beta-2$ is another. Do you see how that implies that $\Bbb{Q}(\beta)$ is then the splitting field? The explanation as to how I found that polynomial is longer .... :-) – Jyrki Lahtonen Mar 28 '17 at 11:01
  • And $$\beta=-1-2\big(\cos(2\pi/19)+\cos(16\pi/19)+\cos(14\pi/19)\big)$$ is one of the zeros. You can actually verify that with a straightforward but longish calculation with roots of unity. Then $$\beta^2+3\beta-2=-1-2\big(\cos(4\cdot2\pi/19)+\cos(4\cdot16\pi/19)+\cos(4\cdot14\pi/19)\big).$$ – Jyrki Lahtonen Mar 28 '17 at 11:05
  • @JyrkiLahtonen emailed you the relevant chapter from Cox, Galois Theory – Will Jagy Mar 29 '17 at 16:01
  • See also http://math.stackexchange.com/questions/1767252/expressing-the-roots-of-a-cubic-as-polynomials-in-one-root. – lhf Mar 30 '17 at 17:47

1 Answers1

1

I guess Jyrki wanted me to post something here. Gauss initiated a study of cyclotomic fields in the Disquisitiones. I found a modern treatment in chapter 9 of Galois Theory by David A. Cox.

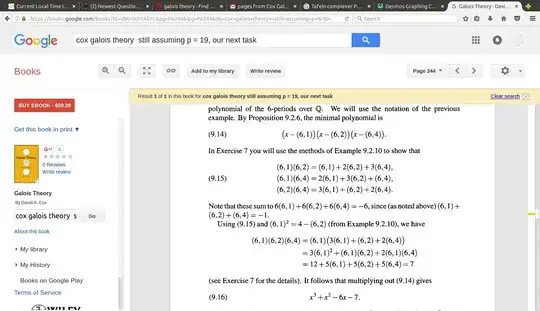
If we begin with your polynomial $g(x) = x^3 + 2 x^2 -5x +1 ,$ then we take $$ f(x) = - g(-x-1) = x^3 + x^2 - 6x - 7. $$ This example is given on page 26 of Reuschle and page 244 of Cox. Given a 19th root of unity $\alpha,$ the three roots, which are real, are expressed as sums of powers of $\alpha.$ Furthermore, these are always paired as a root plus its reciprocal, resulting in cosines.

$$ \eta_0 = 2 \cos \left( \frac{2 \pi}{19} \right) + 2 \cos \left( \frac{14 \pi}{19} \right) + 2 \cos \left( \frac{16 \pi}{19} \right) \approx 2.5070 $$ $$ \eta_1 = 2 \cos \left( \frac{4 \pi}{19} \right) + 2 \cos \left( \frac{6 \pi}{19} \right) + 2 \cos \left( \frac{10 \pi}{19} \right) \approx -2.2851 $$ $$ \eta_2 = 2 \cos \left( \frac{8 \pi}{19} \right) + 2 \cos \left( \frac{12 \pi}{19} \right) + 2 \cos \left( \frac{18 \pi}{19} \right) \approx -1.221 $$

Note that Reuschle provides some multiplications, $$\eta_0^2 = 4 - \eta_1, \; \; \eta_0 \eta_1 = -1 + \eta_1 + 2 \eta_2, \; \; \eta_0 \eta_2 = -1 + \eta_0 + 2 \eta_1 $$ Getting there: $$ \eta_1 \eta_2 = -4 - \eta_0 -3 \eta_1 - 2 \eta_2, $$ $$\eta_1^2 = 4 - \eta_2,$$ $$ \eta_2^2 = \frac{1}{2} \left( 11 + \eta_0 + 3 \eta_1 + 3 \eta_2 \right). $$ Symmetric things $$ \eta_0 + \eta_1 + \eta_2 = -1, $$ $$ \eta_1 \eta_2 + \eta_2 \eta_0 + \eta_0 \eta_1 = -6, $$ $$ \eta_0 \eta_1 \eta_2 = 7, $$ $$ \eta_0^2 + \eta_1^2 + \eta_2^2 = 13, $$ $$ \eta_0^3 + \eta_1^3 + \eta_2^3 = 2. $$ enter image description here

enter image description here

enter image description here

I can emphasize how very straightforward it is to prove the roots work, when given in this fashion. In the following, just use the relation $t^{19} = t^{38} = 1$ to arrive at $$ 11(t^{18} + t^{17} +t^{16} +t^{15} +t^{14} +t^{13} +t^{12} +t^{11} +t^{10} +t^9 +t^8 + t^7 + t^6 + t^5 + t^4 + t^3 + t^2 +t+1) $$

? x = t + t^7 + t^8 + (1/t) + ( 1/t^7) + ( 1/t^8)
%2 = (t^16 + t^15 + t^9 + t^7 + t + 1)/t^8
? p = x^3 + x^2 - 6 * x - 7
%3 = (t^48 + 3*t^47 + 3*t^46 + t^45 + 3*t^41 + 7*t^40 + 8*t^39 + 7*t^38 + 3*t^37 + 3*t^34 + 8*t^33 + 11*t^32 + 11*t^31 + 8*t^30 + 3*t^29 + t^27 + 7*t^26 + 11*t^25 + 11*t^24 + 11*t^23 + 7*t^22 + t^21 + 3*t^19 + 8*t^18 + 11*t^17 + 11*t^16 + 8*t^15 + 3*t^14 + 3*t^11 + 7*t^10 + 8*t^9 + 7*t^8 + 3*t^7 + t^3 + 3*t^2 + 3*t + 1)/t^24
? q = p * t^24
%4 = 
t^48 + 3*t^47 + 3*t^46 + t^45 + 3*t^41 + 7*t^40 + 8*t^39 + 
7*t^38 + 3*t^37 + 3*t^34 + 8*t^33 + 11*t^32 + 11*t^31 + 8*t^30 + 3*t^29 + 
t^27 + 7*t^26 + 11*t^25 + 11*t^24 + 11*t^23 + 7*t^22 + t^21 + 3*t^19 + 
8*t^18 + 11*t^17 + 11*t^16 + 8*t^15 + 3*t^14 + 3*t^11 + 7*t^10 + 
8*t^9 + 7*t^8 + 3*t^7 + t^3 + 3*t^2 + 3*t + 1
?
Will Jagy
  • 139,541