Field of decomposition of $x^3-x^2-4x-1.$ over $\mathbb{Q}$

Question

Suppose we have $f(x)=x^3-x^2-4x-1$ and $\alpha \in \mathbb{C}$ a root of $f(x)$. (We do not know the value of $\alpha$.) It is easy to see that $f(x)$ is irreducible in $\mathbb{Q}[x]$.

It is also easy to prove $-\frac{1}{1+\alpha}$ is also a root of $f(x)$. I need to show $\mathbb{Q}(\alpha)$ is the decomposition field of $f(x)$. Since $f(x)$ is separable, we have three distinct roots $\alpha,-\frac{1}{1+\alpha}, \gamma$. So the decomposition field is $\mathbb{Q}(\alpha,-\frac{1}{1+\alpha}, \gamma)=\mathbb{Q}(\alpha, \gamma)$. How do I show that this is actually equal to $\mathbb{Q}(\alpha)$ without actually calculating the roots of $f(x)?$

Answer 1

Notice that the sum of all the roots equals the coefficient at $x^2$, e.g. $-1$. So $\gamma$ can be expressed in polynomial terms of $\alpha$.

Answer 2

You already have two excellent answers by Jef and Will, but I really do think it is worth mentioning a method that you can just memorise and apply mindlessly in future situations.

Let $\alpha$, $\beta$ and $\gamma$ be the three roots of your irreducible cubic. The Galois group is a subgroup of the permutation group on $ \{ \alpha, \beta, \gamma \}$. Furthermore, the Galois group acts transitively on the roots, since the cubic is irreducible. So there are two possibilities:

• The Galois group is $S_3$, in which case the degree of the extension is six, so the splitting field is larger than $\mathbb Q(\alpha)$.
• The Galois group is $A_3$, in which case the degree of the extension is three, so the splitting field is equal to $\mathbb Q(\alpha)$.

To distinguish between the two cases, consider the discriminant of the cubic: $$ \Delta = (\alpha - \beta)^2(\beta - \gamma)^2(\gamma - \alpha)^2.$$

• If the Galois group is $S_3$, then the odd permutations in $S_3$ send $\sqrt{\Delta} \mapsto - \sqrt{\Delta}$, so $\sqrt{\Delta}$ is not fixed by the Galois group, hence $\sqrt{\Delta} \notin \mathbb Q$.
• If the Galois group is $A_3$, then the Galois group only contains even permutations, which all send $\sqrt{\Delta} \mapsto + \sqrt{\Delta}$, so $\sqrt{\Delta}$ is fixed by the Galois group, hence $\sqrt{\Delta} \in \mathbb Q$.

There is a formula for the discriminant in terms of the coefficients of the cubic. If the cubic is $$ f(x) = x^3 + bx^2 + cx + d,$$ then the discriminant is $$ \Delta = b^2 c^2 - 4c^3 -4b^3 d - 27d^2 + 18bcd. $$ [Note that this simplifies to $\Delta = -4c^3 - 27 d^2$ if $b = 0$, which is easy to remember.]

In your example, $\Delta = 169$, so $\sqrt{\Delta} = 13 \in \mathbb Q$, hence the Galois group is $A_3$, hence the splitting field is $\mathbb Q(\alpha)$.

Needless to say, your method and the answers by Will and Jef show far more ingenuity than what I have suggested, but still I think it's good to have a reliable tool that you can always fall back upon.

Answer 3

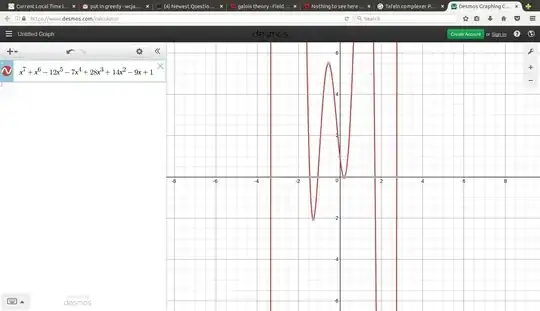
Just for laughs, the roots are $$ 2 \cos \left( \frac{\pi}{13} \right) + 2 \cos \left( \frac{5\pi}{13} \right), $$ $$ 2 \cos \left( \frac{3\pi}{13} \right) + 2 \cos \left( \frac{11\pi}{13} \right), $$ $$ 2 \cos \left( \frac{7\pi}{13} \right) + 2 \cos \left( \frac{9\pi}{13} \right). $$

Reuschle uses $x^3 + x^2 - 4 x + 1$ which is what you get by the method of Gauss, see page 15, jpeg below. I recommend Galois Theory by David A. Cox, chapter 9 for a modern exposition. Method introduced by Gauss in Section VII of the Disquisitiones, some 30 years before Galois Theory. Gauss did few examples, it does take some practice.

Why not: here is a jpeg from the AbeBooks site, showing how to order Reuschle(1875) as a paperback on-demand reprint. The reprint is from a free online source, they don't have a big library of actual old books there at the printing location. I really prefer having actual books to read rather than just on a computer screen.

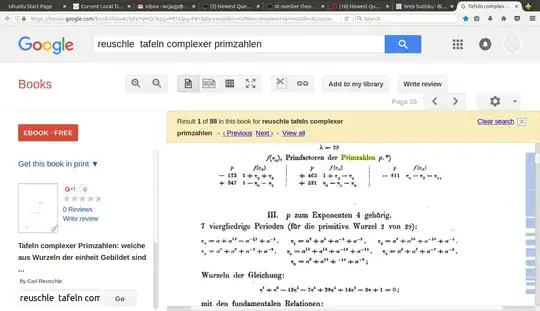
I wrote programs in November and December (2016) to do this. So, here is the whole song and dance for degree 7, prime 29:

jagy@phobeusjunior:~$ ls -l | grep septic | grep greedy
-rwxrwxr-x  1 jagy jagy   370501 Dec  4 14:11 septic_cyclic_gauss_greedy
-rw-rw-r--  1 jagy jagy    23990 Dec  4 14:12 septic_cyclic_gauss_greedy.cc
-rw-rw-r--  1 jagy jagy    23989 Dec  4 14:12 septic_cyclic_gauss_greedy.cc~
jagy@phobeusjunior:~$ 



jagy@phobeusjunior:~$  ./septic_cyclic_gauss_greedy  29
 g to the e  12
    1   12    generator  
    2   28
    3   17    generator  
    1   12   17   28
   a   2

 h1  
    1   12   17   28
 h2  
    2    5   24   27
 h4  
    4   10   19   25
 h8  
    8    9   20   21
 h16  
   11   13   16   18
 h32  
    3    7   22   26
 h64  
    6   14   15   23


=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=

  h1_1     4    0    1    0    0    2    0    0
  h1_2     0    1    0    1    0    0    1    1
  h1_4     0    0    1    0    1    1    1    0
  h1_8     0    0    0    1    2    0    1    0
 h1_16     0    2    0    1    0    0    0    1
 h1_32     0    0    1    1    1    0    0    1
 h1_64     0    0    1    0    0    1    1    1

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=

   h1_1     4    0    1    0    0    2    0    0
   h2_2     4    0    0    1    0    0    2    0
   h4_4     4    0    0    0    1    0    0    2
   h8_8     4    2    0    0    0    1    0    0
 h16_16     4    0    2    0    0    0    1    0
 h32_32     4    0    0    2    0    0    0    1
 h64_64     4    1    0    0    2    0    0    0

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=

 constant               1              0              0              0              0              0              0              0
 linear               0              1              0              0              0              0              0              0
 fifth                 0            100             11             50             15              5             25             50

 sixth               400             21            225             56            105            300            126             91

 seventh                84           1225            294            756            392            189            477            742


7  sofar               84           1225            294            756            392            189            477            742


6  sofar              484           1246            519            812            497            489            603            833

 fourth                36              0             16              1              4             24              6              4

 cubed                 0              9              0              3              0              0              1              3

 squared               4              0              1              0              0              2              0              0
5  sofar              484             46            387            212            317            429            303            233

 table  
       1       3/4         0       1/4    -233/4

       1       1/6         0       1/6    -101/2

       1         0      1/12      1/24    -143/8

       1         0         0       1/4    -317/4

       1         3         0         1      -212

       1         0      1/16      1/16   -387/16


=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=

       1         0         0         0        -7

       0         1         0         0        28

       0         0         1         0        14

       0         0         0         1      -289

       0         0         0         0         0

       0         0         0         0         0

4  sofar              232             46            275            205            289            261            261            205

3  sofar              232            298            275            289            289            261            289            289

2  sofar              288            298            289            289            289            289            289            289

1  sofar              288            289            289            289            289            289            289            289

0  sofar              289            289            289            289            289            289            289            289

 confirm               0              0              0              0              0              0              0              0

  x^7 + x^6 - 12 x^5 - 7 x^4 + 28 x^3 + 14 x^2 - 9 x + 1
 constant 289
   p  29 p.root  2 exps 12^k 
 list of the 4 exponents 
       1      12      17      28


   $$   x^7 + x^6 - 12 x^5 - 7 x^4 + 28 x^3 + 14 x^2 - 9 x + 1, \; \;  p = 29, \; \;  r = 2, \; \; 12^k  $$


gp-pari: 

  x^7 + x^6 - 12 * x^5 - 7 * x^4 + 28 * x^3 + 14 * x^2 - 9 * x + 1


 x = t + (1/t)  + t^12 + (1/t^12)

jagy@phobeusjunior:~$ 

parisize = 4000000, primelimit = 500509
? f = x^7 + x^6 - 12 * x^5 - 7 * x^4 + 28 * x^3 + 14 * x^2 - 9 * x + 1
%1 = x^7 + x^6 - 12*x^5 - 7*x^4 + 28*x^3 + 14*x^2 - 9*x + 1
? polroots(f)
%2 = [
-3.347297326211866604824677822 + 0.E-28*I, 
-1.453219237250277575521353021 + 0.E-28*I, 
-1.063840303785358166816481464 + 0.E-28*I, 
 0.1723984388388905398234384116 + 0.E-28*I, 
 0.2395267590849948773703028220 + 0.E-28*I, 
 1.700463948582122544295969145 + 0.E-28*I, 
 2.751967720741494385672801928 + 0.E-28*I]~
? 

some of these roots are $$ 2 \cos \left( \frac{2 \pi}{29} \right) + 2 \cos \left( \frac{24 \pi}{29} \right) = 2 \cos \left( \frac{2 \pi}{29} \right) - 2 \cos \left( \frac{5 \pi}{29} \right) \approx 0.239526759 $$ $$ 2 \cos \left( \frac{4 \pi}{29} \right) + 2 \cos \left( \frac{48 \pi}{29} \right) = 2 \cos \left( \frac{4 \pi}{29} \right) + 2 \cos \left( \frac{10 \pi}{29} \right) \approx 2.75196772 $$ $$ 2 \cos \left( \frac{8 \pi}{29} \right) + 2 \cos \left( \frac{96 \pi}{29} \right) = 2 \cos \left( \frac{8 \pi}{29} \right) - 2 \cos \left( \frac{9 \pi}{29} \right) \approx 0.1723984 $$ $$ 2 \cos \left( \frac{16 \pi}{29} \right) + 2 \cos \left( \frac{192 \pi}{29} \right) = -2 \cos \left( \frac{13 \pi}{29} \right) - 2 \cos \left( \frac{11 \pi}{29} \right) \approx -1.06384 $$ $$ 2 \cos \left( \frac{32 \pi}{29} \right) + 2 \cos \left( \frac{384 \pi}{29} \right) = -2 \cos \left( \frac{3 \pi}{29} \right) - 2 \cos \left( \frac{7 \pi}{29} \right) \approx -3.347297326 $$ $$ 2 \cos \left( \frac{64 \pi}{29} \right) + 2 \cos \left( \frac{768 \pi}{29} \right) = 2 \cos \left( \frac{6 \pi}{29} \right) + 2 \cos \left( \frac{14 \pi}{29} \right) \approx 1.70046 $$ $$ 2 \cos \left( \frac{128 \pi}{29} \right) + 2 \cos \left( \frac{1536 \pi}{29} \right) = 2 \cos \left( \frac{12 \pi}{29} \right) - 2 \cos \left( \frac{ \pi}{29} \right) \approx -1.4532 $$

Answer 4

Let f:=x^3-x^2-4x-1. It is easy to see that f is an irreducible polynomial over Q. In fact, the degree of f is 3 and so if we prove that f hasn't rational roots, we can conclude that f is irreducible (over Q). Since 1 and -1 are not zeros of f, f is then irreducible.

Now, a is a root of f. You can easy proved that b=:-1/(1+a) is also a root of f. And so, the third root is: c= -1/(1+b) or equivalently: -1/((-1)^3 * ab) = -(1+a)/a. Since the degree of f is odd, f has at least one real root. Since f is separable (f is irreducible and the characteristic of Q is zero), f has not multiple roots. And so: a, b and c are three (simple) real roots. Q(a) is then the splitting field of f over Q (because b and c are clearly elements in Q(a)) and Q(a)/Q is a Galois extension. I hope this helps you. I am very sorry for my bad English.