To find the area in a polar curve, we use areas of sectors of tiny pie slices to figure out the area, to get $$A=\int_a^b\frac{1}{2}r^2\,d\theta$$ Why can't we use the circumference of the circle to figure out arc length of a polar curve? I tried and it went something like this: The arc length of a tiny pie slice is $r\theta$, where theta is in degrees and r is the radius. Adding up all the tiny pie slice arc lengths, we should get $$\int_a^b r\,d\theta$$ But that is clearly not correct! For example, for $1+cos\theta$, this 'formula' tells us that the arc length is $2\pi$, when the actual arc length is 8. What am I doing wrong? Am I assuming something wrong? Or is it just stupid mistakes?
-
2This doesn't work for the same reason that you can't find the length of a curve $y=f(x)$ by integrating $\int_a^b\mathrm dx$. See also "Is value of $\pi=4$?" – Mar 17 '17 at 17:01
-
Note that $\frac{1}{2}r^2 \neq r $, so you should be assuming something wrong. – ChemiCalChems Mar 17 '17 at 17:02
-
1@ChemiCalChems: the OP does not think that $\frac{1}{2}r^2=r$. The expression $\frac{1}{2}r^2$ appears in an integral about the area bounded by a polar curve; the OP is trying to give an analogous argument for arc length, not asserting that $\frac{1}{2}r^2=r$. – symplectomorphic Mar 17 '17 at 17:04
-
@symplectomorphic Completely misread the post. Thanks for the correction. – ChemiCalChems Mar 17 '17 at 17:04
-
I disagree with Rahul's comment a little. The real answer to your question is in the accepted answer here: http://math.stackexchange.com/questions/760757/arc-length-in-polar-coordinates-why-isnt-ds-r×d-theta?rq=1 – symplectomorphic Mar 17 '17 at 17:06
-
The error in the approximation $\delta A\approx \frac{1}{2}r^2\delta\theta$ is second order, while in $\delta s\approx r\delta \theta$, it is of the same order as the approximation. – vnd Mar 17 '17 at 17:10
2 Answers
$\int_0^{2\pi} r\ d\theta$ will give you the average value of $r\cdot 2\pi$
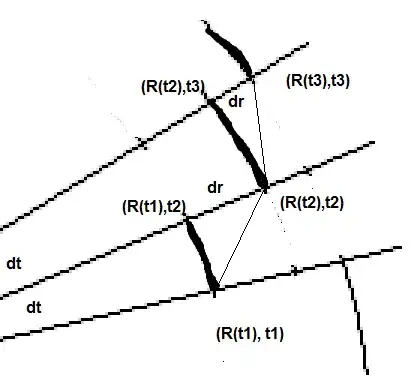
Arc Length in polar coordinates
In the figure, I have taken a curve in Polar coordinates which I have broken up into pieces. If we calculate $\int_0^{2\pi} r\ d\theta$ we will get the sum of the dark lines. It will give you the average value of $r,$ times the range of $\theta$ but it will underestimate the arc length
If you want the arc length, you are going to need the diagonals. in that figure.
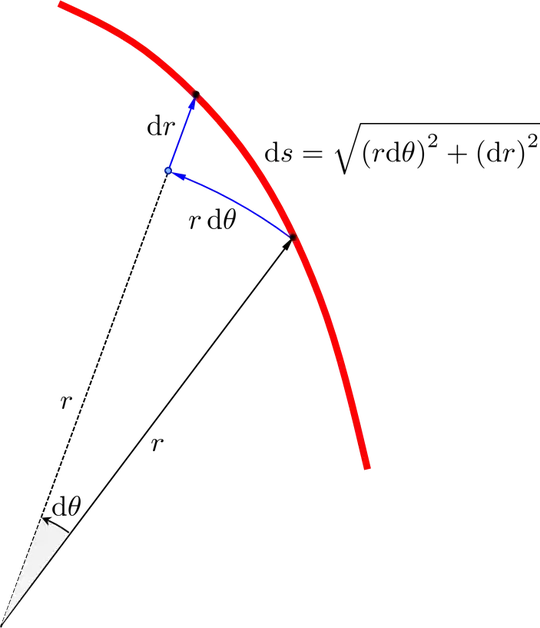
What is the length of the diagonal. As $d\theta$ becomes small, they are aproximately right triangles with one leg $r\ d\theta$ and the other leg, $dr$
And hypotenuse $\sqrt {(r\ d\theta)^2 + (dr)^2)}$
$\int \sqrt {(r^2 + (\frac{dr}{d\theta})^2} \ d\theta$ will give you the arc length
- 57,877
-
1How come this minor little differences don't affect the area integral? How come they only affect the arc length, but using area, they can be ignored/dealt with? – D.R. Mar 18 '17 at 00:09
-
When calculating the areas, we can prove that as $d\theta$ gets small enough $dr$ goes to $0.$ But in the arc length calculation making $d\theta$ very small does not cause $\frac {dr}{d\theta}$ to go to $0$ – Doug M Mar 18 '17 at 00:20
It is the pythagorean theorem that gives as the arc length for a curve in any coordinates.
Consider a small segment ${\rm d}s$ starting from $(r,\theta)$ and going to $(r+{\rm d}r,\theta + {\rm d}\theta)$. As you see in the diagram below the distance due to the angle change is $r {\rm d}\theta$ and the distance due to the radius changing is ${\rm d}r$. Those need to added vectorially to get the displacement of the curve ${\rm d}s$.
- 13,816