Why is it that I cannot imagine a tesseract?

Question

I try hard to "visualise" (say "imagine") a tesseract but I can't.

Why is it that I can't?

---

This may be a question for a scholar of some other discipline and not for a mathematician, e.g. psychology (topic: cognition?), anthropology, etc., but I am sure it is well defined and answerable as a question.

It could be answered with a definition of what I can imagine or the definition of what I can't imagine and why, for example.

There may be some fundamental property of our geometry that limits what we can represent so the question may be interpreted mathematically... anyway I think it is not a question to bounce without any thought.

Specifically: what is missing for me to be able to imagine a tesseract? Understanding? A different kind of brain, that processes information in a different way?

Can a top mathematician visualise a tesseract? I am not inviting a discussion, which would be off-topic. I am soliciting a thoughtful and articulate answer, if possible.

Note:

I already saw this question:

In what sense is a tesseract (shown) 4-dimensional?

and this video:

http://www.youtube.com/watch?NR=1&feature=endscreen&v=uP_d14zi8jk

already read this link:

http://en.wikipedia.org/wiki/Tesseract

and I have studied calculus-level maths, etc. and I found no difficulty in reasoning about imaginary numbers, infinite quantities and/or series, demonstrations ad absurdum, etc.

---

I would be really disappointed if this question were marked as "not constructive", or anything to that effect. I can accept it may be "off topic" because it may relate to how our brain visualises and not some mathematical property that prevents visualisation, but it really should not be considered as "not-constructive". It would actually help me so much to understand this conundrum...

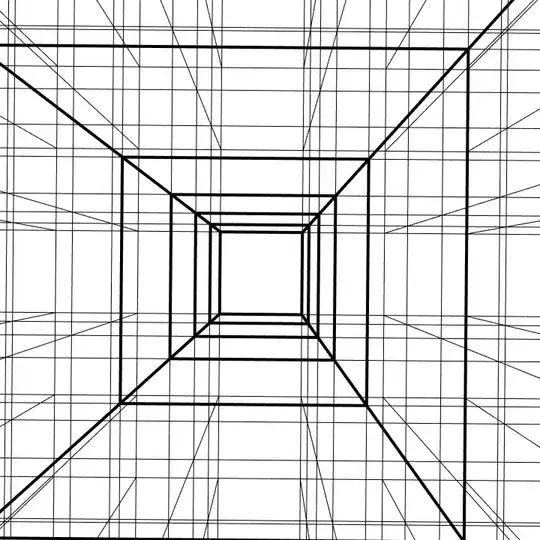
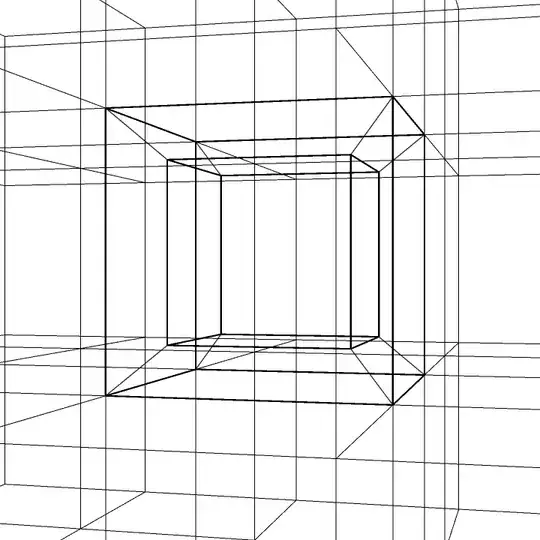Answer 1

Big surprise: our brains evolved in a three-dimensional environment, and so that is what they are best suited for thinking about. It's easy to visualize because we literally see it all the time.

Thinking in higher dimensions is harder because we have no (little?) direct experience with them, so there is not a clear prototype for most people to use as a springboard for visualizing it.

Answer 2

From 2D to 3D

To get an idea of what a 4-cube could look like I started imagining being a 2 dimensional entity on a page containing the projection of a 3-D cube :

$\qquad\qquad\qquad\qquad\qquad$

When my 2D entity progresses in the (new) 'perpendicular' direction to the 'back' of this strange 3-square the square at the middle will appear larger and larger until replacing the external square (a new square will 'materialize' at the middle, seem to grow, and so on...).
Notice that the entity is not moving in its support square and that this square will simply advance in the perpendicular direction without changing size : the growing part is only an effect of perspective!
An actual 3D-entity would cover a continuum of contiguous parallel squares.

Crossing the whole 3D space :

---

From 3D to 4D

Let's try this in 4D : we consider a 3D cube like the previous one and represent a smaller cube inside the first one. Again we imagine that, as we progress in the new perpendicular direction, the smaller cube will grow until taking the place of the larger one ; a new one will appear at the center, grow and so on... Here too we remain at a fixed position of our support cube which will cross other identical cubes while moving in the perpendicular direction.
An actual 4D-entity should occupy a continuum of contiguous cubes.

To move in 'full-4D' you may imagine that cubes are filling the whole 3D space (generating a 3D grid).

Superpose to this 3D grid a smaller and parallel one (or an infinity of smaller and larger ones if you want...) that has a junction at every vertex with the corresponding vertex of the larger one. This will give you a 4D grid and as you move in 4D the smaller grid will take the place of the larger one, a new small grid will get out of the 'mist', grow and so on...

(4D grid variant)

At this point you may imagine moving in your 3D cube or turning around it (changing only the perspective effect) and even the more confusing 4D rotations.

Excellent visualizations !

Answer 3

The key to the answer to this question is already in the word "visualize": It contains "visual", which refers to seeing. Indeed, when you visualize something, you quite literally activate the same structures in your brain that you would also activate when seeing it. You are actually, in a quite direct sense, putting it in front of your "inner eye". Note that also in "imagine" there's the word "image", which also refers to seeing.

This can be seen(!) in a few self-experiments. First, visualize a common item. Let's say a teapot. When you put this teapot in front of your inner eye, you see it the same way you would if you were looking at it. In particular, you'll see the outside, but not the inside (unless you mentally go inside the imagined teapot, in which case you see the inside, but not the outside). Also, you see the side facing you, but not the opposite side.

Now imagine the teapot getting smaller and smaller. For a real shrinking teapot, as it reaches the boundary of your vision, it will lose structure until it ends up as a little point. And you'll notice that the same will happen with your imagined teapot. Note that I'm assuming that you really imagine it shrinking; you can of course instead keep its size in your imagination and put a "mental label" on it "like this, but much smaller". But you cannot imagine, in the literal sense, a microscopically small teapot with all its structure.

Or in other words, strictly speaking you cannot even visualize Euclidean space.

Now the answer to your question is obvious: You cannot visualize the tesseract because you cannot see it. Our eyes do projections of the three-dimensional space into the two-dimensional spaces of our retinas, and our brain then interprets those two images. The tesseract doesn't live in that three-dimensional space projected onto our retinas.

So does this mean we're out of luck? Well, not completely. While in nature there are no tesseracts to see, and no extended four-dimensional space to see in which they could be put, we can do a mathematical projection of the tesseract into three-dimensional space, and then use computers and our visual apparatus (and, after some experience, also our imagination) to make mental images of those projections, while using our abstract understanding together with our three-dimensional intuition/experience on how projections from 3D to 2D behave, to interpret those projections.

Using this method, it is indeed possible to develop a certain feeling for some aspects of four-dimensional objects, like the tesseract. However note that it will never be as natural as the three-dimensional experience which our brain explicitly evolved for (because our ancestors would not have survived without a sufficient understanding of three-dimensional space).

Answer 4

The vertices of a tesseract may be thought of as consisting of the $16$ points of $\{0,1\}^4=\{(a,b,c,d) : a,b,c,d\in \{0,1\}\}$. Two vertices are adjacent (connected by an edge) if and only if their coordinates disagree in exactly one place. For instance, $(0,1,1,0)$ is adjacent to each of the four vertices $(1,1,1,0), (0,0,1,0), (0,1,0,0), (0,1,1,1)$.

Thus each vertex has degree $4$ pointing in mutually orthogonal directions. The direction of an edge is determined by which coordinate its vertices disagree in. This allows us to say which edges are parallel. For instance, the edge joining $(0,1,0,0)$ to $(0,1,1,0)$ is parallel to the edge joining $(1,0,0,0)$ to $(1,0,1,0)$ since in both edges, the vertices disagree in the third coordinate.