3

By drawing a cube on a paper or by seeing it on a screen (a 2D surface - see Figure below), we can sort of visualise how a 3D cube would look like.

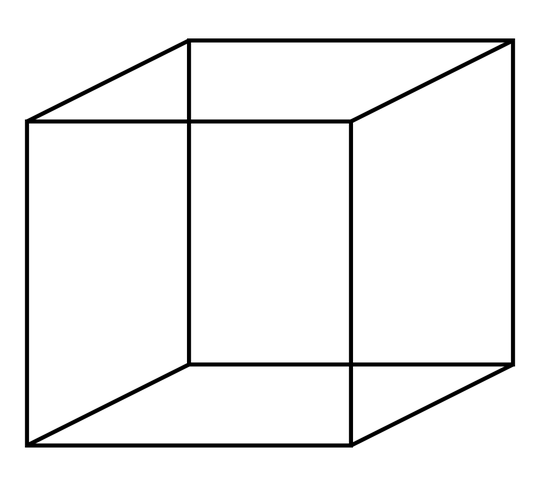
3D cube on a 2D surface - Image from Wikipedia

I was wondering whether we will be able to visualise the tessaract (4D cube) if we build a 3D model of it? However, if we are able to, it will contradict the common belief that one (as a 3D organism) cannot visualise the 4th Dimension. This leads to the question below.

Question: What is the fundamental difference between seeing the 4th dimensions in 3-dimensions and seeing the 3rd dimension in 2D view that stops us from being able to extend our understanding of the 3D to 4D?

Well, some thoughts so far is that to visualize depth in 3D, we use light/shading (for example a 3D object looks lighter nearer to the edge and darker in the centre). The 4th dimension is time/duration, so a question would whether we can make use of time (e.g. moving the object through time???) to help us visualise the 4th dimension better??? If so, how and if not, why not?

rschwieb
  • 153,510
Happytreat
  • 746
  • 1
  • 6
  • 16
  • You are looking at the wrong direction (time). What you can put down on a piece of paper is always a projection, or in some cases, a slice of higher dimensional objects. By studying properties of the projection (just like what people do with engineering drawings), it is not impossible to investigate properties of higher dimensions. I admit that such a viewpoint might be wrong and needs a much rigorous proof otherwise. – Troy Woo Oct 01 '14 at 09:42
  • There are extraordinary minds, such as that of H.S.M. Coxeter, that easily visualize higher dimensional geometry. But I guess this is no longer the sort of visualization you mean, but rather an abstract mathematical visualization. – Troy Woo Oct 01 '14 at 09:45
  • No, it is not a duplicate question because over here I am asking for the fundamental differences between viewing the 4D in 3D lenses and viewing the 3D in 2D lenses. I am not asking why we can't visualise in 4D but rather asking for explanation to the analogy or the logic that i have conjured that led to a contradiction. – Happytreat Oct 01 '14 at 10:11
  • These links might help you have an intuition: - Visualizing 4D Hypercube Data By Mapping Onto a 3D Tesseract - Methods for Visualizing 4D Polytopes – nullgeppetto Oct 01 '14 at 09:44

1 Answers1

4

It is all based on our imagination.

As you say, we are $3$D organisms, and as such, we have visual memories and experiences from a $3$D world. This $2$D drawing of a cube is not similar at all to a real cube, but the image created in our brains while watching it resembles the one we get when watching an actual $3$D cube. Thus, as far as we can tell (with our limited senses), the $2$D cube and the real one are similar to one another.

Unfortunately, we don't meet $4$D objects in our daily life, thus we don't have any visual memories of them. So no picture we see can remind us of a $4$D cube, simply because we don't bear in our minds any image of it.

Yes, we could use time for viewing the $4$th dimension. For example, one can think of $S^3$ as a $2$-sphere that starts from a point, gets bigger and bigger, then smaller and smaller again, until it is reduced again to a point.

Amitai Yuval
  • 19,308