2

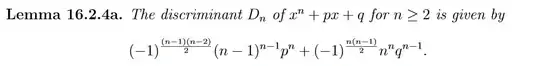
Here is a proof http://www.csie.ntu.edu.tw/~b01902113/artin-sols.pdf and the proof is on page 84. I am searching for help to prove lemma 16.2.4a which is: enter image description here

I am able to follow the prove before the author conclude that $r(n)=s(n−1)$. I am not able to derive $r(n)=s(n-1)$ from the formula above.

And after this, I cannot follow the argument in this whole partenter image description here

I cannot understand what $g(n)$ actually is andhow can we get $(-1)^{\frac{n(n-1)}{2}}\prod_{i=1}^{n}\prod_{i \ne j}(\xi_{i}-\xi_{j})$

I know maybe there are just some algebraic manipulations but I am not able to get them so far.Could someone please explain? Thanks in advance!

Y.X.
  • 3,995
  • Is this not a duplicate of this older question? I would vote to close, but A) my vote is instantly binding, and B) I answered that older version, so it would not be kosher. – Jyrki Lahtonen Feb 27 '17 at 13:39
  • @JyrkiLahtonen I think instead of asking for a full proof, I am searching for explaination to certain steps which I cannot understand. Instead of turing out to any other solutions, I think I do need this version of the proof. Thanks for reference. – Y.X. Feb 27 '17 at 19:17

1 Answers1

1

I cannot understand what $g(n)$ actually is

That's a typo, and it should read $s(n)$ instead of $g(n)\,$. From the previous paragraph:

$$\,D_n (p, q) = s(n−1)\,p^n + s(n)\,q^{n−1}\,$$

Writing it for $\,p=0\,$ and $q=-1\,$ gives:

$$\,D_n (0, -1) = s(n−1) \cdot 0^n + s(n) \cdot (-1)^{n−1}=(-1)^{n-1}\,s(n)\,$$

and how can we get $(-1)^{\frac{n(n-1)}{2}}\prod_{i=1}^{n}\prod_{i \ne j}(\xi_{i}-\xi_{j})$

See this other answer.

Community
  • 1
dxiv
  • 76,497
  • Thanks so much! I can understand why $r(n)=s(n-1)$ now, but there remains 2 identities to prove and I have just asked them http://math.stackexchange.com/questions/2164300/how-can-we-conclude-n-xin-1-prod-i-ne-j-xi-i-xi-j-from-xn-1-p .Could you please prove these 2 identites to enable me to understand the whole proof? – Y.X. Feb 27 '17 at 20:36