8

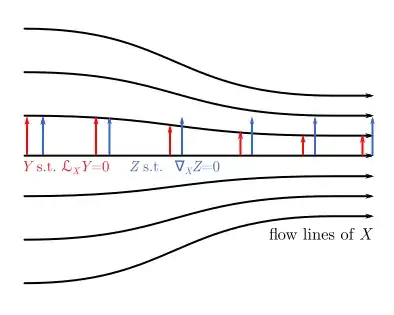
I'm currently teaching a course that "applies" differential geometry to computational problems but doesn't have time to go through theorems/proofs in detail. We're taking a visual approach to help people see from a high level the differential geometry toolbox. I'd like to cover derivatives of vector fields on surfaces. Both the Lie and covariant derivatives come up in such a lecture.

Is there a clear/concrete example of a pair of vector fields $(X,Y)$ on the plane that illustrates (1) why the Lie derivative $\mathcal L_X Y$ is different from the covariant derivative $\nabla_X Y$ and (2) why both derivatives might be useful in different contexts?

I'm looking for a succinct, plot-able visualization to help explain what's going on.

Justin Solomon
  • 880
  • 2
    I found this but it's far from a self contained small example http://math.stackexchange.com/questions/209241/exterior-derivative-vs-covariant-derivative-vs-lie-derivative – Justin Solomon Feb 15 '17 at 14:31
  • The covariant derivative (on a surface in $R^3$) $\nabla_XY$ is at each point the projection on the tangent space at $p$ of the derivative of the field $Y$, viewed as taking values in $R^3$, along the integral curve of $X$ through $p$. This description makes it clear that it is a rather different beast to the Lie derivative, that it depends on the embedding (ie, the metric), and gives it a rather intuitive content. (This interpretation is `half' the content of the so called Gauss formula (the other half is that the normal projection of that derivative is the second fundamental form)) – Mariano Suárez-Álvarez Feb 15 '17 at 14:48
  • [removed response to a comment that's edited] – Justin Solomon Feb 15 '17 at 14:50
  • They differ at essentially all non-silly examples. If you pick your favorite surface, two fields and compute both $[X,Y]$ and $\nabla_XY$, chances are the results will be very different.ç – Mariano Suárez-Álvarez Feb 15 '17 at 14:51
  • Great! Even better if this is for examples on the plane, for which this projected definition of covariant derivative isn't needed. If you could provide one worked-out, this would be much appreciated --- I'm seeking help identifying a very simple example where they're different and the difference suggests why both might be useful. The latter is where I'm a little stuck. Thanks. – Justin Solomon Feb 15 '17 at 14:53
  • I suggest you work out an example. If you get stuck, we can help you get unstuck. This plan will be 17 orders of magnitude more useful for you. – Mariano Suárez-Álvarez Feb 15 '17 at 14:54
  • Haha, indeed I am trying to! This post is here to request help, since this is not a computation I'm terribly comfortable with. I'll continue to work on this but help would be much appreciated; if you do not wish to do so, I understand and will hope someone else might have the time. Thanks! – Justin Solomon Feb 15 '17 at 14:56
  • What vector fields have you picked, on what surface, and where exactly are you stuck in the computation? – Mariano Suárez-Álvarez Feb 15 '17 at 15:01
  • Please give me some time and I'll try to write down the details of what's on my scratch paper (largely frustration...). This is not my area of expertise nor the main topic of our course, and was mainly hoping for someone to help identify a quick example as a side remark (what appears to be a quick computation for you is quite labored for a computer scientist like me! :-) ). I love spending time on exercises like this but sadly the realities of organizing a large course leave little time... – Justin Solomon Feb 15 '17 at 15:09
  • OK @MarianoSuárez-Álvarez, I have posted an answer. Does this look reasonable? A quick check to make sure my calculation isn't totally crazy would be much appreciated (I know it's not the most efficient calculation, but that's alright) – Justin Solomon Feb 15 '17 at 15:44

2 Answers2

18

Here's a qualitative illustration I have lying around, showing the difference between a vector field having zero Lie derivative and zero covariant derivative.

enter image description here

Certainly doesn't capture the whole idea, but might help. I think the main idea I was trying to communicate is that covariant derivatives are all about a single flow line of $X$, while Lie derivatives care about all of $X$.

Anthony Carapetis
  • 35,361
2

At the encouragement of a commenter, I'll post my attempt at a simple example. My apologies if this is completely incorrect.

Take $V(x,y):=(1,-y)$ and $W(x,y):=(-y,x)$, the circular vector field.

To compute the Lie derivative, note that the field $V$ implies a diffeomorphism of the plane $\psi_t(x,y)=(t+x,ye^{-t})$. This effectively warps the $y$ axis.

The Jacobian of $\psi_t$ is: $$ J_t(x,y)=\left( \begin{array}{cc} 1 & 0\\0 &e^{-t} \end{array} \right) $$

Now, let's compute a Lie derivative: $$ \begin{array}{rl} \mathcal L_V W(x,y)&= \lim_{t\rightarrow0}\frac{1}{t} [ (d\psi_{-t})_{\psi_t(p)}(W_{\psi_t(p)})-W_p ]\\ &= \lim_{t\rightarrow0}\frac{1}{t} \left[ \left( \begin{array}{cc} 1&0\\0&e^{t} \end{array} \right) \begin{pmatrix} -ye^{-t}\\t+x \end{pmatrix} - \begin{pmatrix} -y\\x \end{pmatrix} \right] \\ &=\lim_{t\rightarrow0}\frac{1}{t}\begin{pmatrix} -y(e^{-t}-1)\\ e^{t}(t+x)-x \end{pmatrix} \\ &=\begin{pmatrix} y\\1+x \end{pmatrix} \end{array} $$

Because we're in the plane, the covariant derivative coincides with the directional derivative. Hence: $$ \begin{array}{rl} \nabla_VW(x,y) &= \lim_{t\rightarrow0}\frac{1}{t}(W(x+tV_x(x,y),y+tV_y(x,y))-W(x,y)) \\ &= \lim_{t\rightarrow0}\frac{1}{t}(W(x+t,(1-t)y)-W(x,y)) \\ &= \lim_{t\rightarrow0}\frac{1}{t}\begin{pmatrix} -(y-ty)+y\\ (t+x)-x \end{pmatrix} \\ &=\begin{pmatrix} y\\1 \end{pmatrix} \end{array} $$

Notice the $y$ components of these two derivatives differs.

Justin Solomon
  • 880