Prove that these two zeta zero counting functions are essentially the same when not considering the singularities.

Question

I don't know if this is research level or math se level so I try posting here first.

The problem is to prove that the left hand side equals the right hand side for $t>0$ when leaving out singularities such as the points $t$ equal to the imaginary part of a Riemann zeta zero:

$$\left\lfloor \frac{t \log \left(\frac{t}{2 e \pi }\right)}{2 \pi }+\frac{7}{8}\right\rfloor +\frac{1}{2} \left(-1+\text{sgn}\left(\Im\left(\zeta \left(i t+\frac{1}{2}\right)\right)\right)\right)=\frac{\vartheta (t)+\Im\left(\log \left(\zeta \left(i t+\frac{1}{2}\right)\right)\right)}{\pi }$$

Can you prove that the left hand side essentially equals the right hand side for $t>0$ when not considering the singularities?

$\text{sgn}$ is the sign function and the floor function is the down square brackets. $\zeta(s)$ is the Riemann zeta function and $\vartheta(t)$ is the Riemann Siegel theta function.

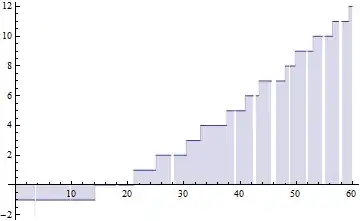
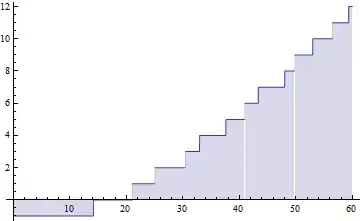
Two plots to verify the similarity between the left hand side and the right hand side:

(*Mathematica 8*)
Plot[(Sign[Im[Zeta[1/2 + I*t]]] - 1)/2 + 
  Floor[t/(2*Pi)*Log[t/(2*Pi*Exp[1])] + 7/8], {t, 0, 60}, 
 Filling -> 0]

Left hand side:

 (*Mathematica 8*)
 Plot[(RiemannSiegelTheta[t] + 
 Im[Log[Zeta[1/2 + I*t]]])/Pi, {t, 0, 60}, Filling -> 0]

Right hand side:

Related: https://oeis.org/A135297

The LHS comes from the estimation of the density of zeros, by the argument principle applied to $\xi(s) = s (s-1)\pi^{-s/2} \Gamma(s/2)\zeta(s)$. We get a term $O(1/t)$ term coming from $\text{arg }\Gamma(s/2)$ , and a term $O(\ln t)$ coming from $\text{arg }\zeta(s)$. Yes the $O(1/t)$ term corresponds to $\vartheta(t)$ — reuns, Feb 09 '17 at 14:35
And the most important is how you define $\text{arg } \zeta(s)$ i.e. $\log \zeta(s)$ : analytic on $Re(s) > 1$, real on $s > 1$ and analytic around $(it-\infty,it+\infty)$ for any $t$ not the imaginary part of a zero. See any book on $\zeta(s)$. — reuns, Feb 09 '17 at 14:43
Ok, this the second time I hear about the argument principle in relation to the left hand side. I thought it was due to Franca-LeClair, but the other person said it is due to Riemann. — Mats Granvik, Feb 09 '17 at 14:46
It is due to Riemann, and Littlewood, and ... You need to read the books on $\zeta(s)$, and work on the mentioned complex analysis theorems ($\zeta(s)$ is an analytic function !!!) — reuns, Feb 09 '17 at 14:49
Wait I didn't read $\text{sgn}(Im(\zeta (\frac{1}{2}+i t)))$ well. I don't know what it is supposed to be, it is not correct — reuns, Feb 09 '17 at 14:55

Mats Granvik · Answer 1 · 2017-05-13T09:36:12.203

This not yet a full answer, but my starting point was this empirical observation:

(*Mathematica 8 start*)Clear[n, k, t, z, FL, NZ]
Print["Set this number kk to 128 and you will get an error message in \
the integration:"]
kk = 127
nn = kk + 1;
FL[n_] = 2*Pi*Exp[1]*Exp[ProductLog[(n - 11/8)/Exp[1]]];
NZ[t_] = RiemannSiegelTheta[t]/Pi + Im[Log[Zeta[1/2 + I*t]] + I*Pi]/Pi;
Monitor[b = -N[
    Table[1 + 
      2*Sum[(NZ[FL[k + 1]] - 1) - (NZ[FL[k]] - 1) - 1, {k, 1, n}], {n,
       0, nn}]], n]
a = Monitor[Table[-Sign[Im[Zeta[1/2 + I*FL[n]]]], {n, 1, Length[b]}], 
  n]
a - Round[b]

where a - Round[b] equals zero for all n>0.

Prove that these two zeta zero counting functions are essentially the same when not considering the singularities.

1 Answers1

Linked