I've found the following derivative in my Calculus book and I can't get my my head around the algebra involved. Can anybody help me?
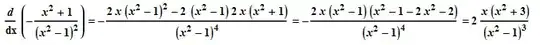
Thanks.
I've found the following derivative in my Calculus book and I can't get my my head around the algebra involved. Can anybody help me?
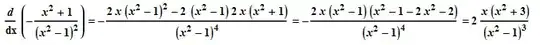
Thanks.
\begin{align*} \frac{d}{dx}\left(-\frac{x^2+1}{(x^2-1)^2}\right) &= -\frac{d}{dx}\left(\frac{x^2+1}{(x^2-1)^2} \right)&\quad&\mbox{(1)}\\ &= -\left(\frac{(x^2-1)^2(x^2+1)' - (x^2+1)\left((x^2-1)^2\right)'}{\left((x^2-1)^2\right)^2}\right)&&\mbox{(2)}\\ &= - \frac{(x^2-1)^2(2x) - (x^2+1)\left(2(x^2-1)(x^2-1)'\right)}{(x^2-1)^4}&&\mbox{(3)}\\ &= -\frac{2x(x^2-1)^2 - (x^2+1)(2(x^2-1)2x)}{(x^2-1)^4}&&\mbox{(4)}\\ &= -\frac{2x(x^2-1)^2 - 4x(x^2+1)(x^2-1)}{(x^2-1)^4}&&\mbox{(5)}\\ &= - \frac{2x(x^2-1)\left((x^2-1) - 2(x^2+1)\right)}{(x^2-1)^4}&&\mbox{(6)}\\ &= - \frac{2x(x^2-1)\left(x^2-1-2x^2-2\right)}{(x^2-1)^4}&&\mbox{(7)}\\ &= - \frac{2x(x^2-1)(-x^2-3)}{(x^2-1)^4}&&\mbox{(8)}\\ &= - \frac{2x(-x^2-3)}{(x^2-1)^3}&&\mbox{(9)}\\ &= -\frac{-2x(x^2+3)}{(x^2-1)^3}&&\mbox{(10)}\\ &= -(-2)\frac{x(x^2+3)}{(x^2-1)^3}&&\mbox{(11)}\\ &= 2\frac{x(x^2+3)}{(x^2-1)^3}.&&\mbox{(12)} \end{align*}
Notes.
The only nontrivial simplification employed in your derivation is reducing the fraction by cancelling the common factor $\rm\ (x^2+1)\:.\:$ You can simplify this by first computing the derivative generically, i.e. compute the general formula for the derivative of $\rm\ f/g^n\ $, then perform the cancellation in the simpler general form, before specializing $\rm\:f,g\:$ to their values. Namely
$$\rm\displaystyle \bigg(\frac{f}{g^n}\bigg)'\ =\ \frac{f\:\:'g^n-n\:f\:g^{n-1}\:g'}{g^{2\:n}} =\ \frac{f\:\:'g-n\ f\ g'}{g^{n+1}}$$
Now, specializing $\rm\ n = 2,\ f = -x^2-1,\ g =\: x^2-1 \:,\: $ we find that the arithmetic is a bit simpler, since we have already cancelled the common factor $\rm\:g^{n-1}\:,\:$ it being glaringly obvious in the simpler generic form.
While this "generic preprocessing" is a bit trivial here, it can provide immense simplifications in other contexts,$\ $ e.g. $\: $ see this proof of $\ $ Sylvester's identity $\rm\ \ det(1+AB) = det(1+BA)\ $ that proceeds by taking $\rm\ det\ $ of $\rm\ (1+A\ B)\ A\ =\ A\ (1+B\ A)\ $ then generically cancelling $\rm\ det(A)\:.\ \ $ This cancellation of the "apparent singularities" where $\rm\:det(A) = 0\:$ is much less trivial than the cancellation of $\rm\: g^{n-1}\: $ in the above derivative calculation. Indeed, most non-generic proofs of Sylvester's identity usually resort to far less elementary non-algebraic methods to deal with such singularities (for example, topological proofs that appeal to ideas based upon density arguments). $\ $ Moral: a little generic thought can go a long way towards avoiding dense proofs.
Just try using the quotient rule for derivatives and see where you get stuck on the algebra. I'm guessing the book just skipped over some intermediate steps and that's why it's not immediately clear how it got to one step to the other. I suggest trying it out on your own first with pencil and paper, then ask again if you get stuck.