Proving $1 \geq \frac{\sin(\theta)}{\theta} \geq \frac{2}{\pi}$ for $\theta \in [0,\frac{\pi}{2}]$

Question

In proving Jordan's lemma, the inequality $$1 \geq \frac{\sin(\theta)}{\theta} \geq \frac{2}{\pi}$$ is used, for $\theta \in [0,\frac{\pi}{2}]$.

I got as far as establishing $1 \geq \sin(\theta) \geq 0$ and $\theta^{-1} \in [\frac{2}{\pi}, \infty)$.

I'm looking for a modest hint.

Are you sure it is $\frac{\pi}{2}$ and not $\frac{2}{\pi}$ in the inequality? Note that $\frac{\pi}{2} > 1$... — Clement C., Jan 25 '17 at 16:10
Yes, you're right; I'll correct it. Thank you for pointing it out. — Mussé Redi, Jan 25 '17 at 16:12
Draw a unit circle, put a point on it in the first quadrant and compare the height to the arc length above the horizontal axis. Note also that $\frac{\pi}{2}>1$ — Paul, Jan 25 '17 at 16:12
@Paul I presume you mean arc height, as opposed to arc length. — Mussé Redi, Jan 25 '17 at 16:24
@Musse Redi the arc length is $\theta$ in the unit circle and clearly $sin(\theta)<\theta$. — Paul, Jan 25 '17 at 20:22

Clement C. · Accepted Answer · 2017-01-25T16:17:00.147

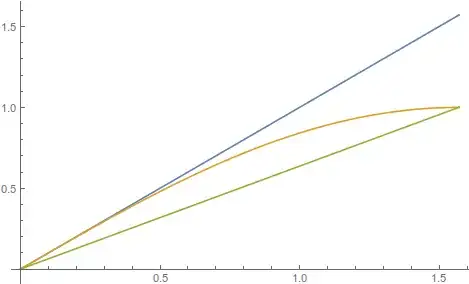
Modest hint: use convexity (actually, here, concavity) of the function $\sin$ on $[0,\frac{\pi}{2}]$.

Followup hint: (place your mouse on the hidden text to reveal it)

A concave function is below its tangents and above its "secants" (linear functions obtained by joining two points of its graph).

Followup hint: (place your mouse on the hidden text to reveal it)

By concavity, $\sin x \leq \sin 0 + \sin'(0)x$ (tangent at $0$) and $\sin x \geq \frac{2}{\pi}$ (line joining $(0,\sin 0)$ and $(\frac{\pi}{2}, \sin \frac{\pi}{2}$).

Here is an illustration showing the three graphs ($x\mapsto x$, $x\mapsto \sin x$, $x\mapsto \frac{2}{\pi}x$):

Proving $1 \geq \frac{\sin(\theta)}{\theta} \geq \frac{2}{\pi}$ for $\theta \in [0,\frac{\pi}{2}]$

1 Answers1