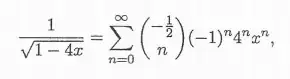Calculation of C(-1/2, n)

Question

I have to represent the function on the left as a power series, and this is the solution to it but I don't know how to calculate this for example when n=1?

$\displaystyle{{-1/2 \choose n} = {n - 3/2 \choose n}\left(-1\right)^{n}}$ — Felix Marin, Jan 21 '17 at 21:55
$\displaystyle{{-1/2 \choose n} = \left(-,{1 \over 4}\right)^{n} {2n \choose n}}$ — Felix Marin, Jan 21 '17 at 22:02

score 0 · Answer 1 · answered Jan 21 '17 at 17:58

0

The formula for $n$ positive integer applies too:

$${n\choose k}=\frac{n(n-1)\cdots(n-k+1)}{k!}$$

regardles whether $n$ is integer or not. It works even for complex $n$. More details here

answered Jan 21 '17 at 17:58

Momo

16,027

score 0 · Answer 2 · answered Jan 21 '17 at 17:58

By definition

$${-\frac{1}{2} \choose 2}=\frac{-\frac{1}{2}(-\frac{1}{2}-1)}{2!}$$

Notice $2$ terms in numerator.

$${-\frac{1}{2} \choose 3}=\frac{-\frac{1}{2}(-\frac{1}{2}-1)(-\frac{1}{2}-2)}{3!}$$

Notice $3$ terms in numerator.

But also remember ${ -\frac{1}{2} \choose 0}=1$.

score 0 · Accepted Answer · answered Jan 21 '17 at 18:00

The symbol ${\alpha \choose n}$ is defined by :

$${\alpha \choose n}=\frac{\alpha(\alpha-1)\cdots(\alpha-n+1)}{n!}$$

So :

$${{-\frac{1}{2}}\choose0}=1\qquad{{-\frac{1}{2}}\choose1}=-\frac{1}{2}\qquad{{-\frac{1}{2}}\choose2}=\frac{\left(-\frac{1}{2}\right)\left(-\frac{1}{2}-1\right)}{2}=\frac{3}{8}$$

and so on ...

Calculation of C(-1/2, n)

3 Answers3