Let $(a_n)$ be a sequence such that $\lim\limits_{N\to\infty} \sum_{n=1}^n |a_n-a_{n+1}|<\infty$. Show that $(a_n)$ is Cauchy.
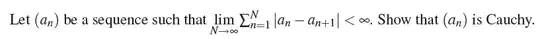
So basically I am told that the sum of the difference isn't infinite. I know that to show the sequence is Cauchy, the difference between the sums must be very small ($\epsilon$). So what exactly do I have to do to answer this question? I am not having a good understanding what "new" information is giving me
Think of it this way: Let $b_n=|a_n-a_{n+1}|$. Then the statement is that $\lim_{N\rightarrow \infty}\sum_{n=1}^N b_n$ is finite, i.e. the series converges. Think about what that implies for $\sum_{n=n_1}^{n_2} b_n$ for large $n_1$ and $n_2$, and then consider how $\sum_{n=n_1}^{n_2} b_n$ compares to $|a_{n_2}-a_{n_1}|$ (which is what you're trying to get very small.)
We will use the fact, if a series $\sum_{k=1}^{\infty} b_k$ converges, then $$ \lim_{n \to \infty}\sum_{k=n}^{\infty} b_k = 0 \,, \quad (1)\,. $$
To prove a sequence $a_n$ is a Cauchy sequence, the following has to hold $$ \lim_{n \to \infty}|a_n-a_{n+p}|=0\,, \quad \forall p\geq 1 \,.$$
Now, applying that to your problem, observe that, $$|a_n-a_{n+p}| = |(a_n-a_{n+1})+(a_{n+1}-a_{n+2})+(a_{n+2}-a_{n+3})+\dots+(a_{n+p-1}-a_{n+p})|$$ $$\implies |a_n-a_{n+p}| = \left|\sum_{k=n}^{n+p-1}(a_k-a_{k+1})\right| \leq \sum_{k=n}^{n+p-1}|a_k-a_{k+1}|\leq \sum_{k=n}^{\infty}|a_k-a_{k+1}|\,, \quad (*) $$ The last inequality follows from the fact that we are adding positive terms. Taking the limit of both sides of $(*)$ and using $(1)$, the desired result follows
$$ \lim_{n \to \infty}|a_n-a_{n+p}|=0\,, \quad \forall p\geq 1\,. $$
What do you know about the tails of converging series? How can you use that information to bound the distances between points in the Cauchy sequence?
