4

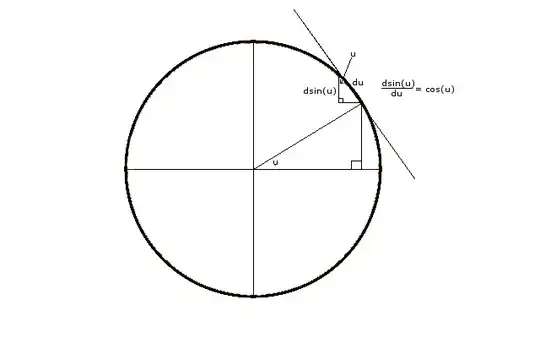
Is this the correct way to make this visualization of the derivative of sine more... rigorous? At least, for $u\in(0,\pi/2)$.

enter image description here

Borrowed from Proofs without words. To try to make this rigorous, I argued that when $u\pm\Delta u$ is in the first quadrant, that we have the following geometrically obtained bounds:

$$\frac{\sin(u+\Delta u)-\sin(u)}{\Delta u}<\cos(u)<\frac{\sin(u-\Delta u)-\sin(u)}{-\Delta u}$$

where $\Delta u>0$. From this, I thought that the derivative of sine comes trivially, though I am wondering if this could be more rigorous.

Community
  • 1
Simply Beautiful Art
  • 74,685
  • A rigorous argument must establish the fact that $\lim_{x \to 0}\dfrac{\sin x}{x} = 1$. The diagram in your post only gives an intuitive argument as to why the derivative of $\sin x$ should be $\cos x$ and I don't think one can improve upon this further. – Paramanand Singh Jan 08 '17 at 16:27
  • :-( Aw, that would've been pretty interesting @ParamanandSingh – Simply Beautiful Art Jan 08 '17 at 16:35

1 Answers1

1

As I mentioned in my comment, it is not possible to add rigor into the existing figure given in your question. Note that the diagram if drawn correctly shows that the angle marked $u$ in the smaller triangle is actually slightly greater than $u$. More precisely we know that $$\sin (u + \Delta u) - \sin u = 2\cos \left(u + \frac{\Delta u}{2}\right)\sin\frac{\Delta u}{2}$$ and noting the inequality $\sin x < x$ we see that $$\frac{\sin(u + \Delta u) - \sin u}{\Delta u} < \cos\left(u + \frac{\Delta u}{2}\right)$$ Further note that a proof based on a geometrical figure is not necessarily non-rigorous, rather there are such geometrical proofs which are fully rigorous. The lack of rigor in the current scenario comes not from geometry but from wrong interpretation of geometrical figure so that an angle which is not exactly $u$ is marked / interpreted as $u$.

Community
  • 1
Paramanand Singh
  • 87,309