1

I know that proving the $\lim\limits_{x\to0} \frac{\sin(x)}{x}$ another way is true but my question is from this proof (1) on proofwiki.

Is the method they use to proof the equation invalid? It seems to create circular logic as you can see in at the beginning of this video on youtube.

Also from the following:

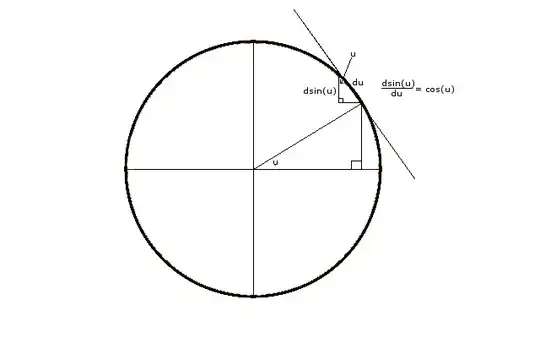
Statement A: $\,\frac{d}{dx} \sin(x)\big|_{x=0} = 1$

Statement B: $\,\sin(x) = \sum_{k=0}^\infty \tfrac{(-1)^k x^{2k+1}}{(2k+1)!}$

Statement C: $\,\lim\limits_{x \to 0} \tfrac{\sin(x)}{x} = 1$

Here is the problem:

$$A\implies B\implies C\implies A$$ This is a circular.

So the method of proof (1) on the proofwiki site is a false method?

They use infinite sum which is taylor series of $\sin(x)$ which requires the derivative of $\sin(x)$ which creates circular logic?

Or it is still true provided the infinite sum of $\sin(x)$ derives from a taylor series centred at another point not $0$.

In this case can we avoid taking derivative of $\sin(x)$ at $0$ ?

So on the proof (1) they should add condition that sin(x) derive from taylor series centred not at $0$? Am I understanding this correctly?

When you take the series as a definition of $\sin$, that's taylor's theorem

"In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point."

So to avoid that should we think that statement $B$ is derived from taylor series centred not at $0$?

Please also watch the video provided in the question. It also has circular logic problem.

Please provide an easy understanding and step by step answer. I'm a newbie in calculus $2$ and have no more knowledge than calculus $2$.

user3270418
  • 793
  • Can you just take the series as a definition of $\sin$ instead of a result derived by Taylor's theorem? – velut luna Aug 09 '16 at 10:09
  • when you take the series as a definition of sin, that's taylor's theorem. https://en.wikipedia.org/wiki/Taylor_series : "In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point.". So to avoid that is to think as derived from taylor series centred not at 0 ??? – user3270418 Aug 09 '16 at 10:11
  • 1
    Interesting question, I would like to know if you can arrive at the infinite series another way. – User0112358 Aug 09 '16 at 10:11
  • I can't see why taking the series as definition is just Taylor's theorem. You just need to show that it is well-defined. – velut luna Aug 09 '16 at 10:14
  • the coefficient of the series (the -1^n) comes from derivative of sin(x) (if you look at how this series derive from) which means it is circular logic unless you think of deriving it as taylor series centred at a when a is not equal to 0 – user3270418 Aug 09 '16 at 10:16
  • I mean why you have to derive it? You just define it by the series and show that it is well-defined. – velut luna Aug 09 '16 at 10:19
  • 1
    ProofWiki calls it the definition of the function. But this is not the definition I know: sin(x) extends the ratio of opposite over hypotenuse of a triangle to the the entire circle the triangle is enscribed in, and then wraps around and around. Thus you get a periodic function. The proof I know of the limit in question looks at this nature of the function, and the squeezing theorem. You do all of this BEFORE you know how to differentiate sin(x). Is there another way? Cool if there is. – User0112358 Aug 09 '16 at 10:19
  • OK, if you define $\sin$ by geometry, then I agree that the proof by Taylor's theorem is circular. However, the usual proof by geometry and squeeze theorem is also circular. Of course that depends on how you obtain the formula $A=\pi r^2$. – velut luna Aug 09 '16 at 10:23
  • for @AlphaGo you said "taking the series as definition" so how can you show that sin(x) is equal to the series without differentiation? – user3270418 Aug 09 '16 at 10:24
  • If you agree to take that as a definition, of course they equal!!! – velut luna Aug 09 '16 at 10:25
  • @AlphaGo you said it is equal, can you prove that sin(x) is equal to the series without differentiation? – user3270418 Aug 09 '16 at 10:26
  • You said you agree to take that as the definition of $\sin$ don't you? Then what on earth do you want me to show? – velut luna Aug 09 '16 at 10:27
  • @AlphaGo I didn't said it's equal until I can prove it, but you did said it. if you are not intellectual enough to answer this question properly please don't bother the community by giving unreasonable answers, please leave. – user3270418 Aug 09 '16 at 10:32
  • I've already given you my answer. If you define it by geometry, then the argument by Taylor's theorem is circular. If you define it by the series, then you can show the limit very easily. And you keep asking me to show that the LHS and the RHS are the same in a definition! – velut luna Aug 09 '16 at 10:37
  • Do not re-post. – Daniel Fischer Aug 09 '16 at 11:05
  • Its not repost. This post ask weather the proof is false. The other post ask another aspect. Same equation but ask in different aspect and different topic – user3270418 Aug 09 '16 at 11:11
  • 1
    I've tried to edit you question to make it a bit easier on the eye. I didn't want to remove any of the individual questions as otherwise some of the above comments might not make sense. Please check I haven't changed anything to your dislike. – snulty Aug 09 '16 at 11:52

3 Answers3

4

The proof cannot be circular. One way to do all of this consistently is to define $\sin$, $\cos$ and $e^z$ by power series and then the limits, derivatives and further analytical properties follow from this definition.

However, you may ask then

How does this definition relate to the geometric meaning of $\sin$, $\cos$?

I have been wondering about this as a student and it's a pity that most books avoid this. One way to connect the geometric and algebraic definitions goes as follows:

  • Using the power-series definitions, show (using elementary computations) that $e^{z_1 + z_2}=e^{z_1}e^{z_2}$ and $\overline{e^z}=e^{\overline{z}}$. As a consequence, $|e^{it}|=1$ for real $t$.
  • Consider the curve $\varphi(t)=e^{it}$ and show that the derivative is $\varphi'(t)=i e^{it}$. In particular, $|\varphi'(t)|=1$ and so $\varphi$ represents a movement on the circle with unit speed. There are just two ways how such constant-speed movement is possible: either you rotate counter-clockwise, or clockwise.
  • Note that the movement must be "couter-clockwise" because $\varphi'(0)=+i$.
  • Define $\pi$ to be the smallest positive number for which $\varphi(2\pi)=1$ and show that $\sin$, $\cos$, $e^{it}$ are $2\pi$-periodic (using uniqueness of a solution of the differential equation $\dot{x}(t)= i x(t)$ with an initial condition.)
  • The fact that $\sin$, $\cos$ are projections of $\varphi$ to the real and imaginary axis follows immediately from the power series definition.

There is also a "reversed" way: $\sin$ and $\cos$ and $\pi$ can be defined so that they satisfy a simple set of axioms (all of those reflecting the geometrical intuition) and then one proves that such functions exist, are unique, have the derivatives as required, and then the power series as a result.

Community
  • 1
Peter Franek
  • 11,522
  • Thank you very much for your good detail answer Peter Franek, I hope I could understand all the point you have made but my knowledge is at calculus 2 level. I do not know differential equation and imaginary axis yet. I will come back to your answer after I finish those course. For now can you please answer my simple question on general fact about the proof of this equation from the proofwiki, proofing it the way the proofwiki does in the proof1 is valid or invalid? when you say "define sin by power series" don't you have to use Taylor series to get that power series from sin function? – user3270418 Aug 09 '16 at 13:48
  • as you can see in the statement B, the coefficient of x (the -1^k) comes from taking derivative of sin. or do you have other method rather than using taylor series to get that series (the statement B)? – user3270418 Aug 09 '16 at 13:51
  • @user3270418 It's simpler than you think: on this page, they take the sum to be the definition of $\sin$ and then they derive the limit. Using your notation, they only show that $B\Rightarrow C$, nothing more (at least in "Proof 1"). – Peter Franek Aug 09 '16 at 13:54
  • Can you proof that B is true without using Taylor series? because if you use taylor series to proof that B is true then there is a problem because if we derive it from taylor series centred at 0, it will have circular logic problem unless we derive it from taylor series centred at a where a is not equal to 0 then the whole statement A, B and C are true and the way the proofwiki proof1 is true. math is consistent, we need precise meaning, we can't make our own rule, it has to be consistent. – user3270418 Aug 09 '16 at 14:09
  • Please also watch the video provided in the question. It also has circular logic problem. – user3270418 Aug 09 '16 at 14:38
  • 1
    @user3270418 First of all, I can prove that $B$ is true if you tell me what is $\sin$. Secondly, in the wiki link, they took the $B$ power series for the definition of $\sin$. Do you understand what definition means? – Peter Franek Aug 09 '16 at 17:25
  • @PeterFranek thanks. I'd never seen this before: it is very interesting – User0112358 Aug 10 '16 at 05:55
0

A and C are equivalent (C is the definition of A). B implies A and C but A (or C) does not imply B. It is not stated like this on wiki, either.

H. H. Rugh
  • 35,236
0

Lookie here!

enter image description here

It provides geometric reasoning for why $\frac d{dx}\sin(x)=\cos(x)$. From this, you should easily see that when $x\pm h$ is in the first quadrant, then:

$$\frac{\sin(x-h)-\sin(x)}{-h}<\cos(x)<\frac{\sin(x+h)-\sin(x)}{h}$$

So the derivative follows quite clearly. One can similarly do this for $\cos$ and quite clearly see that

$$\left.\frac d{dx}\sin(x)\right|_{x=0}=\lim_{h\to0}\frac{\sin (h)}h=1$$

And of course, Taylor's theorem follows from all of this.

Simply Beautiful Art
  • 74,685
  • At the risk of being nitpicky, does the inequality you state guarantee that the limit exists? It's clear to me that $\lim\inf_{h\to0^+}\frac{\sin(x+h)-\sin(x)}{h}\ge \cos x$ and that $\lim\sup_{h\to0^-}\frac{\sin(x+h)-\sin(x)}{h}\le \cos x$, but I'm not sure this can be cobbled together to find the derivative. – πr8 Jan 06 '17 at 09:47
  • @πr8 One would need to assume that the derivative exists? Hm... – Simply Beautiful Art Jan 06 '17 at 12:28
  • @πr8 see here: http://math.stackexchange.com/questions/2085417/make-this-visual-derivative-of-sine-more-rigorous – Simply Beautiful Art Jan 06 '17 at 12:29