5

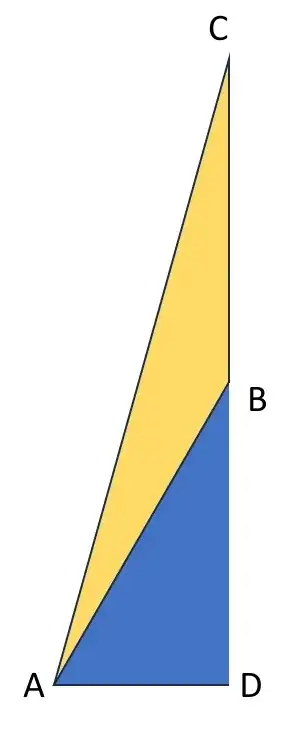
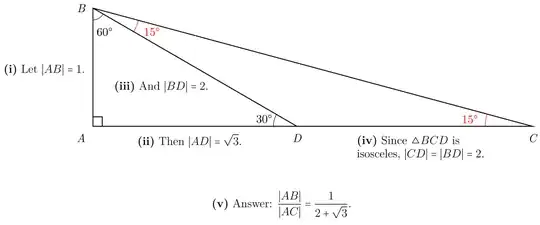
$\text{What is the ratio of legs in a right triangle with angles of 15, 75, and 90?}$ I know the ratio of legs in a $30, 60, 90$ triangle, which is the lengths $1$, $\sqrt{3}$, and $2$ respectively. This is what I have got so far: Using the 30-60-90 Ratio

How would I be able to take this a step further and be able to find the answer? Thanks in advance.

Ojasw Upadhyay
  • 325

5 Answers5

3

The ratio of legs is $$ r = \tan 15^\circ. $$ (This is quite easily derived from the definition of the $\tan$ function.)

You can also represent the ratio using radicals: $$ r = 2 - \sqrt{3} \approx 0.267949 $$

If we do not want to use $\tan$ at all, then we obtain the same answer just reasoning from your picture: $$ r = {1\over2+\sqrt{3}}= 2 - \sqrt{3}. $$

(In this ratio, the numerator $1$ is the vertical leg in your picture; and the denominator $2+\sqrt{3}$ is the horizontal leg.)

Alex
  • 4,873
  • 1
    And I might add: That is a very well-reasoned picture, and good thinking to come up with that answer without any reference to trigonometry. – Wildcard Jan 03 '17 at 23:38
  • Yes. On the other hand, the picture is a nice and easy way to explain why $\tan 15^\circ$ equals $2-\sqrt3$ exactly. – Alex Jan 03 '17 at 23:43
  • 1
    @Alex Thanks a lot for this and I liked how you actually proved that the tan 15 $= 2-\sqrt{3}$. :) – Ojasw Upadhyay Jan 05 '17 at 17:38
1

Let $a$, $b$, $c$ represent the line segments the make up a right triangle, and let $A$, $B$, $C$ represent the angles opposite those line segments. Let $C=90^\circ$

The legs ($a$ and $b$) are given by the following equations. $$a=c\sin{A}$$ $$b=c\cos{A}$$

We want to find the ratio $a\over b$.

$${a\over b}={c\sin{A}\over c\cos{A}}={\sin{A}\over \cos{A}}=\tan(A)$$

Now substitute the value of $A$ in your example. You can either use $15^\circ$ or $75^\circ$ (using one instead of the other will give the inverse ratio).

$${a\over b}=\tan(15^\circ)\quad\text{or}\quad{b\over a}=\tan(75^\circ)$$

pseudoeuclidean
  • 1,012
1

$\triangle ABD$ has a right angle at $D$ and acute angles of $30°(B)$ and $60°(A)$. $\triangle ABC$ is isosceles with base $\overline{AC}$. Thus with the dimensions of the $30°-60°-90°$ right triangle, $BC=AB=2AD$ and $BD=\sqrt3AD$. Also $\angle ACD$ in the isosceles triangle measures half the exterior $\angle ABD$, thus $15°$. Thereby $\triangle ACD$ is a right triangle with acute angles measuring $15°$ and $75°$, with $\color{blue}{CD=BC+BD=(2+\sqrt3)AD}$.

enter image description here

Oscar Lanzi
  • 39,403
1

enter image description here

...........................................................................

-1

See the link here, it provides an explanation of the ratios and has other resources on triangle ratios:

https://robertlovespi.net/2013/10/18/the-15-75-90-triangle/

Brief overview:

15-75-90 triangle is based on the regular dodecagon, using this diagram:

Using the Pythagoran Theorem and other methods, we get the short leg:long leg:hypotenuse ratio in a 15-75-90 triangle as $2-\sqrt{3}:1:2\sqrt{2 - \sqrt{3}}.$ The nested radical ultimately simplifies to $\sqrt{6} - \sqrt{2},$ so the simplified ratio is $2 - \sqrt{3}:1:\sqrt{6} - \sqrt{2}.$

ᴇɴᴅᴇʀᴍᴀɴ
  • 143
  • 1
    The short leg: long leg: Hypotenuse is $2-\sqrt{3}:1:\sqrt{6}-\sqrt{2}.$

    In the website, the nested radical was not simplified.

     – ᴇɴᴅᴇʀᴍᴀɴ Nov 12 '21 at 01:44
  • 1
    Would you be willing to outline the explanation here, for stackexchange? Then we can be sure the information will be here permanently. – 311411 Nov 12 '21 at 02:13
  • "Using the Pythagoran Theorem and other methods" = "and then a miracle occurs". Please tell us more, we like learning about miracles! – Oscar Lanzi Jun 08 '23 at 20:44