1

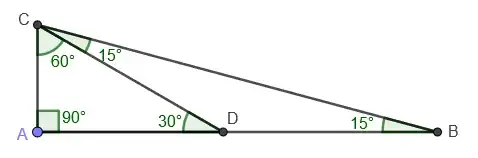
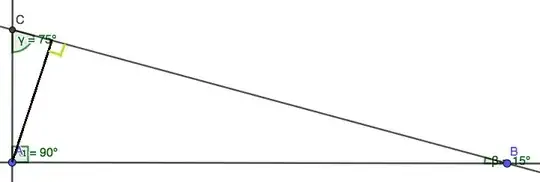
So there is a right triangle $ABC$ with $m∠C=90°$, $m∠B=75°$, and $BC\ (the \ hypotenuse)=12 cm$. I want to find the area of this triangle

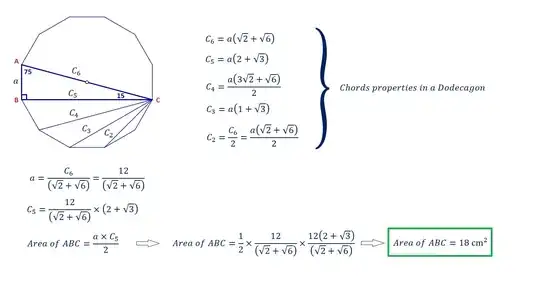
It would look something like this: enter image description here

Note: I have already solved this problem and got the answer as $18$ $cm^2$. So, I am not looking for an answer, I am looking for another way to solve this problem.

I have looked at other stack exchange questions similar to this question that involves $15-75-90$ triangles:

Ex. https://math.stackexchange.com/a/2082666/521593

All of these questions were solved using trigonometric functions however, I think there is a way to solve this using elementary geometry without trigonometric functions. I tried to go somewhere with splitting $∠B$ into $30-60-90$ triangles or a $15-15-150$ triangle but to no avail as it did not help me at all.

If anyone could help, find this way it would be most appreciated. Thanks.

DeepSea
  • 77,651
Atrey Desai
  • 119
  • 1
    It seems to me that you are asking to evaluate the area of this triangle without pushing a trig function key on a calculator, so if I can evaluate some trig function of $15^\circ$ I have solved the problem. Is that what you are thinking? – Ross Millikan Sep 23 '18 at 03:27

3 Answers3

7

Here is your triangle with just one extra segment inscribed in it:

enter image description here

Now you have a $30$-$60$-$90$ triangle, whose ratios you presumably know. That is, you know the ratios of $AC$ and $AD$ to $CD.$ But also $BD=CD$ and $AB = AD + BD,$ so you have the ratio $AB : CD,$ and now you can use the Pythagorean Theorem to get the ratio $BC: CD.$ But $BC = 12,$ and using the ratios you have found you can assign lengths to all the other segments, in particular $AB$ and $AC.$ Then you can find the area.

David K
  • 98,388
  • Thanks, for the triangles, I did not see that before but I am still don't get the ratios. What would the ratio of $AB:CD$ be? Based on what you wrote, I would assume that you can only find out the equation $AB=AD+BD$. Then how would you go to the conclusion that $BC:CD$ using the Pythagorean theorem? I feel that you might have gotten the right answer but that I don't your solution. It would be helpful if you could clarify the questions I have above and describe your solution more. Thanks – Atrey Desai Sep 23 '18 at 22:52
  • 1
    I use ratios like this: if $p:q = 1:3$ and $p:r = 1:4$ then $p:(q+r) = 1:7$, $p^2:q^2 = 1:9,$ and $p:\sqrt{q^2+r^2}=1:5.$ Adding two parts of a segment and applying the Pythagorean theorem to ratios are as easy as that. But if that's too confusing, you could set $CD = x$ (that is, $CD$ is $x$ units long) and label the other segments with things like $x$, $\frac12x,$ $\frac{\sqrt3}2x,$ and so forth until finally you have $BC$ as some number times $x$, and then since $BC=12$ you find the exact value of $x$ and put actual numbers (without $x$) for all the other lengths. – David K Sep 24 '18 at 02:17
3

We can use the chords properties of a Dodecagon: enter image description here

Seyed
  • 8,933
1

Draw a perpendicular from A to the hypotenuse

Now find length of perpendicular using basic trignometry and Area of Triangle = ${1\over2}(BC)(Lenght\ of\ perpendicular)$

Community
  • 1
Awakened
  • 447
  • 3
  • 14
  • 1
    OP asked for a solution without trig, but I think this one can get there if you use similar triangles. Fundamentally we want to evaluate some trig function of $15^\circ$ without pushing the button on the calculator. I think this gives a quadratic that solves the problem. – Ross Millikan Sep 23 '18 at 02:44
  • i think use of the most basic trigonometry is inevitable – Awakened Sep 23 '18 at 02:46
  • we can also do this using vectors but the OP is asking for elementary geometry solution – Awakened Sep 23 '18 at 02:47
  • I don't think so. Your approach will get a trig function of $15^circ$ as a solution to a quadratic. You replace the use of the trig function with the solution to the quadratic you have found. I'll do it if you don't want to, but you had the good idea. Let $C$ to the foot of the perpendicular be $x$. Now use similar triangles and Pythagoras and you will get there. – Ross Millikan Sep 23 '18 at 02:50
  • sorry ,i didn' t understand your comment . Are you saying that the vector approach is not possible?I will try myself then.(for reference- i am class 12th student) – Awakened Sep 23 '18 at 02:55
  • I don't think a vector approach will work because you can't find the coordinates of the triangle corners without trig. Call the foot of the altitude $D$ and $CD=x, DB=12-x$. Now use similar triangles to say $\frac {CD}{AC}=\frac {AC}{12}$ and similar. When you clear the fractions you get $AC^2=12CD$. Plug that into the Pythagorean relations and I think you get there. – Ross Millikan Sep 23 '18 at 03:01
  • The challenge is that you haven't used the fact that the angle is $15^{\circ}$ anywhere. You could draw that altitude in any right triangle. Again all the triangles are similar. We need to relate to an equilateral triangle and essentially use the half angle formula. – Ross Millikan Sep 23 '18 at 03:11
  • area$=|{1\over2}(\overrightarrow{AB}X\overrightarrow{AC})|=|0.512\cos{75}12\cos{15}|=18$ – Awakened Sep 23 '18 at 03:15
  • But we are not given $18$, we are trying to find it. That is why I said we just need to find one trig function of $15^\circ$. From that and reproving some trig identities we are home. It is hard when people say find or prove something without X because we can't use anything that depends on X and we don't keep careful track. Different orders of development can have different things depending on X. – Ross Millikan Sep 23 '18 at 03:22
  • ok , now i got your point. Yeah, its difficult to do this without using trigonometry at all. – Awakened Sep 23 '18 at 03:25