3

I'm working on figuring out how to count the number of distinct partitions in the number N - this set of values http://oeis.org/A000009.

From wikipedia (and other sources), there is a generating function for this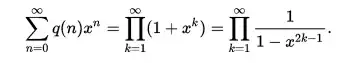enter image description here

What I'm struggling to understand is how I actually go from this function to calculating the number of partitions for some value N. I'll admit I'm not all that familiar with generating functions, but if someone could help me through an example of how we could use this (or if there's another way) to compute the number of distinct partitions where N = 5.

Jeff Storey
  • 141
  • This question recently appeared at this MSE link and also at this MSE link II. For small N you may simply expand the first N terms of the GF. – Marko Riedel Jan 02 '17 at 21:48
  • @MarkoRiedel could you give an example of how that would work for this case? Some of these mathematical constructs are a bit new to me (or it's been a long while since I've studied them). – Jeff Storey Jan 02 '17 at 22:02
  • I have added a proof of the recurrence for strict partitions into any number of parts at this MSE link. Combine with memoization for an efficient means of calculating these numbers. – Marko Riedel Jan 03 '17 at 00:13

1 Answers1

7

To begin with, let us briefly explain the concept of a generating function and how the number of partitions is calculated from this.

Next we discuss why the function given is the right one for the Problem.

1) A generating function of some infinite sequence of numbers $a(n), n = 1, 2, 3, ...$ is defined as

$$g(x)=\sum _{n=1}^{\infty } a(n) x^n$$

This means that a(n) is the coefficient of $x^n$ of the Taylor expansion of g(x) about x = 0.

Hence for N = 5

$$g(x) = \prod _{k=1}^\infty \left(x^k+1\right) = 1 + x + x^2 + 2 x^3 + 2x^4 + 3 x^5 + ...$$

Which means N = 5 has 3 (coefficient of $x^5$) distinct partitions.

2) Consider this product

$$(x+1) \left(x^2+1\right) \left(x^3+1\right) ... $$

Multiplying out gives a sum of terms of the form

$$a(N)x^{k_1+k_2+...} $$

where

$$k_1+k_2+... = N$$

All $k_i$ must be different because they originate from different factors $x^{k_i}$ in the original product. The factor $a(N)$ obviuosly gives the number of possible combinations of terms $x^N$ of the product.

But this in turn is what we whish to calculate, the number of distinct partitions of the number $N$.

Dr. Wolfgang Hintze
  • 12,465